
(本小題滿分13分) 已知等差數列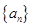 滿足:
滿足: ,
,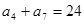 ,
,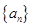 的前n項和為
的前n項和為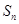 .
.
(Ⅰ)求通項公式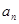 及前n項和
及前n項和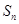 ;
;
(Ⅱ)令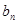 =
=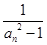 (n
(n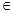 N*),求數列
N*),求數列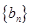 的前n項和
的前n項和 .
.
(Ⅰ)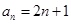 ;
; 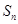 =
=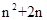 ;(Ⅱ)
;(Ⅱ)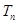 =
=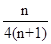 。
。
【解析】
試題分析:(1)結合已知中的等差數列的項的關系式,聯立方程組得到其通項公式和前n項和。
(2)在第一問的基礎上,得到bn的通項公式,進而分析運用裂項法得到。
解:(Ⅰ)設等差數列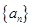 的公差為d,由已知可得
的公差為d,由已知可得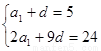 ,
,
解得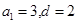 ,……………2分,
,……………2分,
所以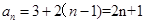 ;………4分
;………4分
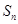 =
=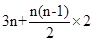 =
=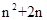 ………6分
………6分
(Ⅱ)由(Ⅰ)知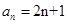 ,
,
所以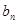 =
=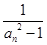 =
=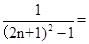
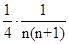 =
=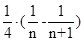 ……10分
……10分
所以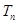 =
=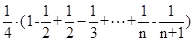 =
=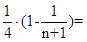
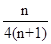
即數列 的前n項和
的前n項和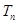 =
=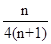 ……13分
……13分
考點:本試題主要考查了等差數列的通項公式以及前n項和的求解運用。
點評:解決該試題的關鍵是能得到等差數列的通項公式,然后求解新數列的通項公式,利用裂項的思想來得到求和。易錯點就是裂項的準確表示。


 小學課堂作業系列答案
小學課堂作業系列答案 金博士一點全通系列答案
金博士一點全通系列答案科目:高中數學 來源:2015屆江西省高一第二次月考數學試卷(解析版) 題型:解答題
(本小題滿分13分)已知函數
 .
.
(1)求函數 的最小正周期和最大值;
的最小正周期和最大值;
(2)在給出的直角坐標系中,畫出函數 在區間
在區間 上的圖象.
上的圖象.
(3)設0<x< ,且方程
,且方程 有兩個不同的實數根,求實數m的取值范圍.
有兩個不同的實數根,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年福建省高三年級八月份月考試卷理科數學 題型:解答題
(本小題滿分13分)已知定義域為 的函數
的函數 是奇函數.
是奇函數.
(1)求 的值;(2)判斷函數
的值;(2)判斷函數 的單調性;
的單調性;
(3)若對任意的 ,不等式恒成立
,不等式恒成立 ,求k的取值范圍.
,求k的取值范圍.
查看答案和解析>>
科目:高中數學 來源:河南省09-10學年高二下學期期末數學試題(理科) 題型:解答題
(本小題滿分13分)如圖,正三棱柱 的所有棱長都為2,
的所有棱長都為2, 為
為 的中點。
的中點。
(Ⅰ)求證: ∥平面
∥平面 ;
;
(Ⅱ)求異面直線 與
與 所成的角。www.7caiedu.cn
所成的角。www.7caiedu.cn

[來源:KS5
U.COM
查看答案和解析>>
科目:高中數學 來源:2010-2011學年福建省高三5月月考調理科數學 題型:解答題
(本小題滿分13分)
已知 為銳角,且
為銳角,且 ,函數
,函數 ,數列{
,數列{ }的首項
}的首項 .
.
(1) 求函數 的表達式;
的表達式;
(2)在 中,若
中,若 A=2
A=2 ,
, ,BC=2,求
,BC=2,求 的面積
的面積
(3) 求數列 的前
的前 項和
項和
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com