精英家教網(wǎng)> 2025年學(xué)典四川九年級數(shù)學(xué)全一冊北師大版 > 第2頁 參考答案
2025年學(xué)典四川九年級數(shù)學(xué)全一冊北師大版
注:目前有些書本章節(jié)名稱可能整理的還不是很完善,但都是按照順序排列的,請同學(xué)們按照順序仔細(xì)查找。練習(xí)冊2025年學(xué)典四川九年級數(shù)學(xué)全一冊北師大版答案主要是用來給同學(xué)們做完題方便對答案用的,請勿直接抄襲。
1. 如圖,菱形 $ABCD$ 中,已知 $\angle ABD = 20^{\circ}$,則 $\angle C$ 的度數(shù)是(
D
)
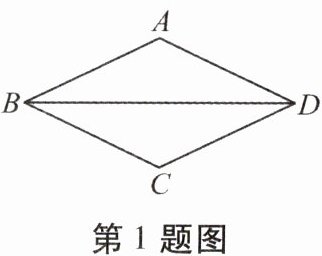
A.$40^{\circ}$
B.$80^{\circ}$
C.$120^{\circ}$
D.$140^{\circ}$
答案:D
解析:
解:在菱形$ABCD$中,$AB = AD$,$\angle A+\angle C=180^{\circ}$。
$\triangle ABD$中,$\angle ABD = 20^{\circ}$,則$\angle ADB=\angle ABD = 20^{\circ}$。
$\angle A=180^{\circ}-\angle ABD-\angle ADB=180^{\circ}-20^{\circ}-20^{\circ}=140^{\circ}$。
$\angle C=180^{\circ}-\angle A=180^{\circ}-140^{\circ}=40^{\circ}$。
A
2. 如圖,在菱形 $ABCD$ 中,點(diǎn) $E$,$F$ 分別是 $AC$,$AB$ 的中點(diǎn),如果 $EF = 3$,那么菱形 $ABCD$ 的周長為(
A
)
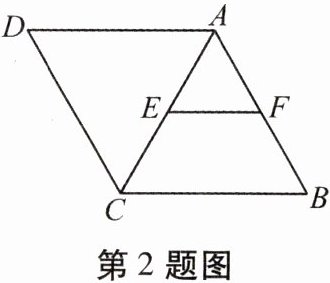
A.$24$
B.$18$
C.$12$
D.$9$
答案:A
解析:
在菱形$ABCD$中,$AB=BC=CD=DA$。
因?yàn)辄c(diǎn)$E$,$F$分別是$AC$,$AB$的中點(diǎn),所以$EF$是$\triangle ABC$的中位線。
根據(jù)三角形中位線定理,$EF=\frac{1}{2}BC$。
已知$EF = 3$,則$\frac{1}{2}BC=3$,解得$BC=6$。
菱形$ABCD$的周長為$4× BC=4×6 = 24$。
A
3. 如圖,菱形 $ABCD$ 對角線的交點(diǎn)與坐標(biāo)原點(diǎn) $O$ 重合,已知點(diǎn) $A$ 的坐標(biāo)為 $(-2,5)$,則點(diǎn) $C$ 的坐標(biāo)是(
B
)

A.$(5,-2)$
B.$(2,-5)$
C.$(2,5)$
D.$(-2,-5)$
答案:B
解析:
在菱形$ABCD$中,對角線互相平分,交點(diǎn)為坐標(biāo)原點(diǎn)$O$,則點(diǎn)$A$與點(diǎn)$C$關(guān)于原點(diǎn)對稱。
已知點(diǎn)$A$的坐標(biāo)為$(-2,5)$,關(guān)于原點(diǎn)對稱的點(diǎn)的坐標(biāo)特點(diǎn)是橫、縱坐標(biāo)均互為相反數(shù),所以點(diǎn)$C$的坐標(biāo)為$(2,-5)$。
B
4. 如圖,在平面直角坐標(biāo)系中,菱形 $OACB$ 的頂點(diǎn) $O$ 與原點(diǎn)重合,若點(diǎn) $C$ 的坐標(biāo)為 $(4,0)$,點(diǎn) $B$ 的縱坐標(biāo)是 $-1$,則菱形 $OACB$ 的頂點(diǎn) $A$ 的坐標(biāo)是______
(2,1)
.

答案:(2,1)
解析:
∵菱形$OACB$的頂點(diǎn)$O$與原點(diǎn)重合,對角線$OC$與$AB$相交于點(diǎn)$D$。
∵點(diǎn)$C$的坐標(biāo)為$(4,0)$,
∴$OC$在$x$軸上,$OC=4$,$OD=\frac{1}{2}OC=2$,即點(diǎn)$D$的橫坐標(biāo)為$2$。
∵菱形的對角線互相平分,
∴點(diǎn)$D$是$AB$的中點(diǎn)。
設(shè)點(diǎn)$A$的坐標(biāo)為$(x,y)$,點(diǎn)$B$的坐標(biāo)為$(m,-1)$。
∵點(diǎn)$D$是$AB$的中點(diǎn),
∴$\frac{x+m}{2}=2$,$\frac{y+(-1)}{2}$為點(diǎn)$D$的縱坐標(biāo)。
又
∵$OC$與$AB$互相垂直平分,$OC$在$x$軸上,
∴$AB$垂直于$x$軸,即點(diǎn)$A$和點(diǎn)$B$的橫坐標(biāo)相同,$x=m$。
由$\frac{x+x}{2}=2$,得$x=2$。
∵$AB$垂直于$x$軸,$D$為$AB$中點(diǎn),$OD=2$,$B$的縱坐標(biāo)為$-1$,
∴$\frac{y+(-1)}{2}=0$($D$在$x$軸上,縱坐標(biāo)為$0$),解得$y=1$。
∴點(diǎn)$A$的坐標(biāo)是$(2,1)$。
$(2,1)$
5. 如圖,在菱形 $ABCD$ 外側(cè)作等邊三角形 $CBE$,連接 $DE$,$AE$。若 $\angle ABC = 100^{\circ}$,則 $\angle EDC$ 的度數(shù)為
$20^{\circ}$
.

答案:$20^{\circ}$
解析:
∵四邊形$ABCD$是菱形,
$\therefore CD = CB$,$\angle ADC=\angle ABC = 100^{\circ}$,$\angle BCD=180^{\circ}-\angle ABC=80^{\circ}$。
∵$\triangle CBE$是等邊三角形,
$\therefore CB = CE$,$\angle BCE=60^{\circ}$。
$\therefore CD=CE$,$\angle DCE=\angle BCD+\angle BCE=80^{\circ}+60^{\circ}=140^{\circ}$。
在$\triangle DCE$中,$CD = CE$,
$\therefore \angle EDC=\frac{180^{\circ}-\angle DCE}{2}=\frac{180^{\circ}-140^{\circ}}{2}=20^{\circ}$。
$20^{\circ}$
6. 如圖,菱形 $ABCD$ 的邊長為 $2$,$\angle ABC = 60^{\circ}$,對角線 $AC$ 與 $BD$ 交于點(diǎn) $O$,$E$ 為 $OB$ 的中點(diǎn),$F$ 為 $AD$ 的中點(diǎn),連接 $EF$,則 $EF$ 的長為
$\frac{\sqrt{13}}{2}$
.
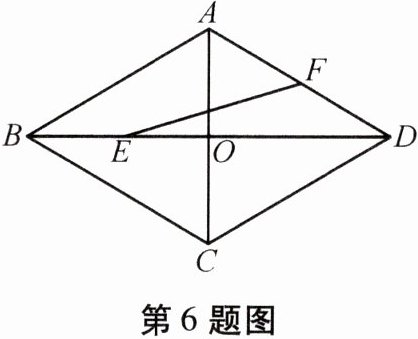
答案:$\frac{\sqrt{13}}{2}$
解析:
解:
∵菱形 $ABCD$ 邊長為 $2$,$\angle ABC=60^\circ$,
∴$\triangle ABC$ 為等邊三角形,$AC=AB=2$,$BD \perp AC$,$O$ 為 $AC$、$BD$ 中點(diǎn),
∴$AO=OC=1$,$BO=DO=\sqrt{AB^2 - AO^2}=\sqrt{2^2 - 1^2}=\sqrt{3}$。
以 $O$ 為原點(diǎn),$AC$ 為 $x$ 軸,$BD$ 為 $y$ 軸建立坐標(biāo)系,
則 $A(-1,0)$,$D(0,\sqrt{3})$,$B(0,-\sqrt{3})$。
∵$E$ 為 $OB$ 中點(diǎn),$F$ 為 $AD$ 中點(diǎn),
∴$E\left(0,-\frac{\sqrt{3}}{2}\right)$,$F\left(\frac{-1+0}{2},\frac{0+\sqrt{3}}{2}\right)=\left(-\frac{1}{2},\frac{\sqrt{3}}{2}\right)$。
∴$EF=\sqrt{\left(-\frac{1}{2}-0\right)^2 + \left(\frac{\sqrt{3}}{2}+\frac{\sqrt{3}}{2}\right)^2}=\sqrt{\left(-\frac{1}{2}\right)^2 + (\sqrt{3})^2}=\sqrt{\frac{1}{4}+3}=\frac{\sqrt{13}}{2}$。
$\frac{\sqrt{13}}{2}$
7. 如圖,在菱形 $ABCD$ 中,$AE \perp CD$,垂足為 $E$,$CF \perp AD$,垂足為 $F$。求證:$AF = CE$。

答案:證明:
∵四邊形ABCD是菱形,
∴AD=CD,∠D=∠D(公共角)。
∵AE⊥CD,CF⊥AD,
∴∠AED=∠CFD=90°。
在△AED和△CFD中,
∠AED=∠CFD,
∠D=∠D,
AD=CD,
∴△AED≌△CFD(AAS)。
∴DE=DF。
∵AD=CD,
∴AD-DF=CD-DE,即AF=CE。







