
科目: 來源: 題型:
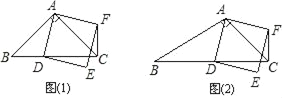
【題目】在△ABC中,∠ACB=45°.點D(與點B、C不重合)為射線BC上一動點,連接AD,以AD為一邊且在AD的右側作正方形ADEF.
(1)如果AB=AC.如圖①,且點D在線段BC上運動.試判斷線段CF與BD之間的位置關系,并證明你的結論.
(2)如果AB≠AC,如圖②,且點D在線段BC上運動.(1)中結論是否成立,為什么?
(3)若正方形ADEF的邊DE所在直線與線段CF所在直線相交于點P,設AC=4![]() ,BC=3,CD=x,求線段CP的長.(用含x的式子表示)
,BC=3,CD=x,求線段CP的長.(用含x的式子表示)
查看答案和解析>>
科目: 來源: 題型:
【題目】某中學計劃購買A型和B型課桌凳共200套,經招標,購買一套A型課桌凳比購買一套B型課桌凳少用40元,,且購買4套A型和6套B型課桌凳共需1820元。
(1)求購買一套A型課桌凳和一套B型課桌凳各需多少元?
(2)學校根據實際情況,要求購買這兩種課桌凳總費用不能超過40880元,并且購買A型課桌凳的數量不能超過B型課桌凳的![]() ,求該校本次購買A型和B型課桌凳共有幾種方案?哪種方案的總費用最低?
,求該校本次購買A型和B型課桌凳共有幾種方案?哪種方案的總費用最低?
查看答案和解析>>
科目: 來源: 題型:
【題目】定義![]() 為一次函數y=px+q的特征數.
為一次函數y=px+q的特征數.
(1)若特征數是![]() 的一次函數為正比例函數,求m的值;
的一次函數為正比例函數,求m的值;
(2)已知拋物線y=(x+n)(x-2)與x軸交于點A、B,其中n>0,點A在點B的左側,與y軸交于點C,且△OAC的面積為4,O為原點,求圖象過A、C兩點的一次函數的特征數.
查看答案和解析>>
科目: 來源: 題型:
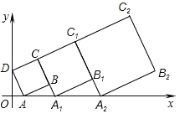
【題目】在平面直角坐標系中,正方形ABCD的位置如圖所示,點A的坐標為(1,0),點D的坐標為(0,2).延長CB交x軸于點A1,作正方形A1B1C1C;延長C1B1交x軸于點A2,作正方形A2B2C2C1…按這樣的規律進行下去,第2012個正方形的面積為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 與
與![]() 軸、
軸、![]() 軸分別交于點
軸分別交于點![]() ,
,![]() ,拋物線
,拋物線![]() 經過點
經過點![]() ,將點
,將點![]() 向右平移5個單位長度,得到點
向右平移5個單位長度,得到點![]() .
.
(1)求點![]() 的坐標;
的坐標;
(2)求拋物線的對稱軸;
(3)若拋物線與線段![]() 恰有一個公共點,結合函數圖象,求
恰有一個公共點,結合函數圖象,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目: 來源: 題型:
【題目】(1)如圖1,點P是等邊△ABC內一點,已知PA=3,PB=4,PC=5,求∠APB的度數.
要直接求∠A的度數顯然很因難,注意到條件中的三邊長恰好是一組勾股數,因此考慮借助旋轉把這三邊集中到一個三角形內.
解:如圖2,作∠PAD=60°使AD=AP,連接PD,CD,則△PAD是等邊三角形.
∴ =AD=AP=3,∠ADP=∠PAD=60°
∵△ABC是等邊三角形
∴AC=AB,∠BAC=60°∴∠BAP=
∴△ABP≌△ACD
∴BP=CD=4, =∠ADC
∵在△PCD中,PD=3,PC=5,CD=4,PD2+CD2=PC2
∴∠PDC= °
∴∠APB=∠ADC=∠ADP+∠PDC=60°+90°=150°
(2)如圖3,在△ABC中,AB=BC,∠ABC=90°,點P是△ABC內一點,PA=1,PB=2,PC=3,求∠APB的度數.
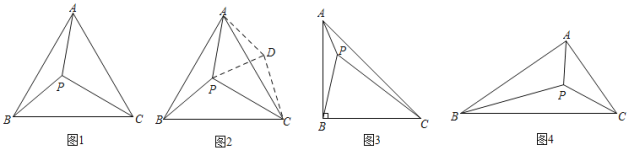
(3)拓展應用.如圖4,△ABC中,∠ABC=30°,AB=4,BC=5,P是△ABC內部的任意一點,連接PA,PB,PC,則PA+PB+PC的最小值為 .
查看答案和解析>>
科目: 來源: 題型:
【題目】已知關于x的一元二次方程x2﹣x+![]() m=0有兩個實數根.
m=0有兩個實數根.
(1)若m為正整數,求此方程的根.
(2)設此方程的兩個實數根為a、b,若y=a(a﹣1)﹣2b2+2b+1,求y的取值范圍.
查看答案和解析>>
科目: 來源: 題型:
【題目】參與兩個數學活動,再回答問題:
活動![]() :觀察下列兩個兩位數的積
:觀察下列兩個兩位數的積![]() 兩個乘數的十位上的數都是9,個位上的數的和等于
兩個乘數的十位上的數都是9,個位上的數的和等于![]() ,猜想其中哪個積最大?
,猜想其中哪個積最大?
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
活動![]() :觀察下列兩個三位數的積
:觀察下列兩個三位數的積![]() 兩個乘數的百位上的數都是9,十位上的數與個位上的數組成的數的和等于
兩個乘數的百位上的數都是9,十位上的數與個位上的數組成的數的和等于![]() ,猜想其中哪個積最大?
,猜想其中哪個積最大?
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 分別寫出在活動
分別寫出在活動![]() 、
、![]() 中你所猜想的是哪個算式的積最大?
中你所猜想的是哪個算式的積最大?
![]() 對于活動
對于活動![]() ,請用二次函數的知識證明你的猜想.
,請用二次函數的知識證明你的猜想.
查看答案和解析>>
科目: 來源: 題型:
【題目】如圖,⊙O的直徑AB為10cm,弦AC為6cm,
(1)用尺規作圖畫出∠ACB的平分線交⊙O于點D.(不要寫作法,保留作圖痕跡)
(2)分別連接點AD和BD,求弦BC、AD、BD的長.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com