精品一区二区免费在线观看_国产精品久久久久久av福利软件_97成人精品区在线播放_国内成人精品一区

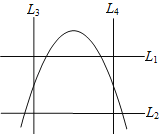
A.l1為x軸，l3為y軸B.l2為x軸，l3為y軸

C.l1為x軸，l4為y軸D.l2為x軸，l4為y軸

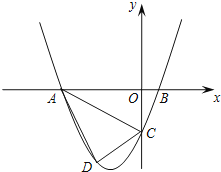
（1）求拋物線的解析式；

（2）若點D是線段AC下方拋物線上的動點，求四邊形ABCD面積的最大值．

【題目】如圖，AB是的直徑，點C、D在上，且AD平分，過點D作AC的垂線，與AC的延長線相交于E，與AB的延長線相交于點F，G為AB的下半圓弧的中點，DG交AB于H，連接DB、GB．

證明EF是的切線；

求證：；

已知圓的半徑，，求GH的長．

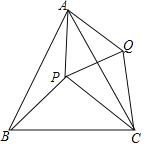
（1）求證：△BAP≌△CAQ．

（2）若PA＝3，PB＝4，∠APB＝150°，求PC的長度．

（1）小紅摸出標有數(shù)3的小球的概率是多少？．

（2）請你用列表法或畫樹狀圖法表示出由x，y確定的點P（x，y）所有可能的結(jié)果．

（3）求點P（x，y）在函數(shù)y=﹣x+5圖象上的概率．

【題目】如圖，拋物線交軸于、兩點，經(jīng)過點，交軸于點．

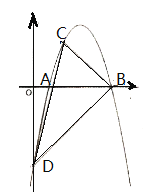
（1）求拋物線的解析式及點的坐標；

（2）求的面積；

（3）若點在直線上，點在平面上，是否存在這樣的點，使得以點為頂點的四邊形為菱形？若存在，請直接寫出點的坐標；若不存在，請說明理由．

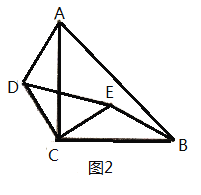
【題目】問題：如圖1，等腰直角三角形中，，點、點分別在邊上，且，顯然．

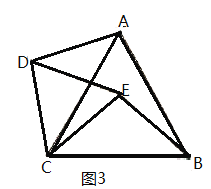
變式：若將圖1中的繞點逆時針旋轉(zhuǎn)，使得點在的內(nèi)部，其它條件不變（如圖2），請你猜想線段與線段的關(guān)系，并加以證明．

拓展：若圖2中的、都為等邊三角形，其它條件不變（如圖3），則__________，直線與相交所夾的銳角為__________°．

【題目】如圖，已知二次函數(shù)的圖象過兩點．

（1）求此二次函數(shù)的解析式；

（2）設(shè)二次函數(shù)的圖象與軸的另一個交點為，求點的坐標；

（3）在同一坐標系中畫出此二次函數(shù)及直線，并寫出當在什么范圍內(nèi)時，一次函數(shù)的值大于二次函數(shù)的值．

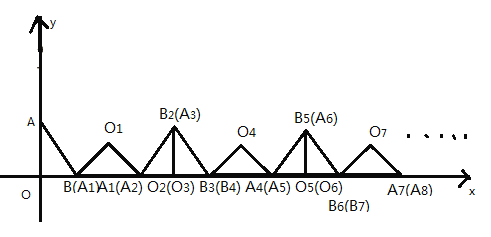
【題目】如圖，等腰直角三角形中，點、點分別在軸、軸上，且． 將繞點順時針旋轉(zhuǎn)使斜邊落在軸上，得到第一個；將繞點順時針旋轉(zhuǎn)使邊落在軸上，得到第二個；將繞點順時針旋轉(zhuǎn)使邊落在軸上，得到第三個；……順次這樣做下去，得到的第2019個三角形落在軸上的邊的右側(cè)頂點所走的路程為___________．

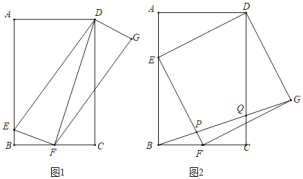
（1）連接DF，求DF的長度；

（2）求DEFG周長的最小值；

（3）當DEFG為正方形時（如圖2），連接BG，分別交EF，CD于點P、Q，求BP：QG的值．