
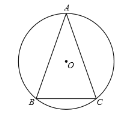
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,圓
,圓![]() 是
是![]() 的外接圓.
的外接圓.
(1)求圓![]() 的半徑;
的半徑;
(2)若在同一平面內(nèi)的圓![]() 也經(jīng)過
也經(jīng)過![]() 、
、![]() 兩點,且
兩點,且![]() ,請直接寫出圓
,請直接寫出圓![]() 的半徑的長.
的半徑的長.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)過點![]() 作
作![]() ,垂足為
,垂足為![]() ,連接
,連接![]() ,根據(jù)垂直平分線的性質(zhì)可得
,根據(jù)垂直平分線的性質(zhì)可得![]() 在
在![]() 上,根據(jù)垂徑定理即可求出BD,再根據(jù)勾股定理即可求出AD,設
上,根據(jù)垂徑定理即可求出BD,再根據(jù)勾股定理即可求出AD,設![]() ,根據(jù)勾股定理列出方程即可求出半徑;
,根據(jù)勾股定理列出方程即可求出半徑;
(2)根據(jù)垂直平分線的判定可得點P在BC的中垂線上,即點P在直線AD上,然后根據(jù)點A和點P的相對位置分類討論,然后根據(jù)勾股定理分別求出半徑即可.
(1)過點![]() 作
作![]() ,垂足為
,垂足為![]() ,連接
,連接![]()

∵![]() ,
,![]()
∴![]() 垂直平分
垂直平分![]()
∵![]()
∴點![]() 在
在![]() 的垂直平分線上,即
的垂直平分線上,即![]() 在
在![]() 上.
上.
∵![]()
∴![]()
∵在![]() 中,
中,![]() ,
,![]()
∴![]()
設![]() ,則
,則![]()
∵在![]() 中,
中,![]() ,
,
∴![]() ,即
,即![]()
解得![]() ,即圓
,即圓![]() 的半徑為
的半徑為![]() .
.
(2)∵圓![]() 也經(jīng)過
也經(jīng)過![]() 、
、![]() 兩點,
兩點,
∴PA=PB
∴點P在BC的中垂線上,即點P在直線AD上
①當點P在A下方時,此時AP=2,如下圖所示,連接PB

∴PD=AD-AP=4
根據(jù)勾股定理PB=![]() ;
;
②當點P在A上方時,此時AP=2,如下圖所示,連接PB
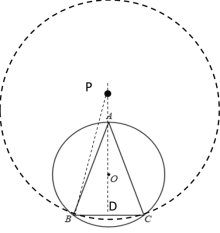
∴PD=AD+AP=8
根據(jù)勾股定理PB=![]() .
.
綜上所述:圓![]() 的半徑的長為
的半徑的長為![]() 或
或![]() .
.


科目:初中數(shù)學 來源: 題型:
【題目】如圖,剪兩張對邊平行且寬度相同的紙條隨意交叉疊放在一起,轉動其中一張,重合部分構成一個四邊形,則下列結論中不一定成立的是( )
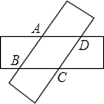
A. ∠ABC=∠ADC,∠BAD=∠BCDB. AB=BC
C. AB=CD,AD=BCD. ∠DAB+∠BCD=180°
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,認真觀察下面這些算式,并結合你發(fā)現(xiàn)的規(guī)律,完成下列問題:
算式①![]() ,
,
算式②![]() ,
,
算式③![]() ,
,
算式④![]() ,
,
…
(1)請寫出:算式③______;算式④______;
(2)上述算式的規(guī)律可以用文字概括為:“兩個連續(xù)奇數(shù)的平方差能被8整除”,如果設兩個連續(xù)奇數(shù)分別為![]() 和
和![]() (
(![]() 為整數(shù)),請說明這個規(guī)律是成立的;
為整數(shù)),請說明這個規(guī)律是成立的;
(3)你認為“兩個連續(xù)偶數(shù)的平方差能被8整除”這個說法是否也成立呢?請說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
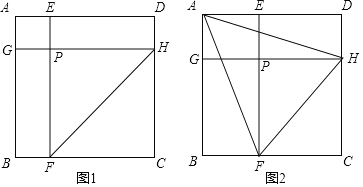
【題目】如圖,邊長為a的正方形ABCD被兩條與邊平行的線段EF、GH分割成四個小矩形,EF與GH交于點P,連接AF、AH、FH.
(1)如圖1,若a=1,AE=AG=![]() ,求FH的值;
,求FH的值;
(2)如圖2,若∠FAH=45°,證明:AG+AE=FH;
(3)若Rt△GBF的周長l=a,求矩形EPHD的面積S與l的關系(只寫結果,不寫過程).
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某商場試銷一種成本為每件![]() 元的服裝,規(guī)定試銷期間銷售單價不低于成本單價,且獲利不得高于
元的服裝,規(guī)定試銷期間銷售單價不低于成本單價,且獲利不得高于![]() ,經(jīng)試銷發(fā)現(xiàn),銷售量
,經(jīng)試銷發(fā)現(xiàn),銷售量![]() (件)與銷售單價
(件)與銷售單價![]() (元)的關系符合一次函數(shù)
(元)的關系符合一次函數(shù)![]() .
.
![]() 直接寫出銷售單價
直接寫出銷售單價![]() 的取值范圍,
的取值范圍,
![]() 若銷售該服裝獲得利潤為
若銷售該服裝獲得利潤為![]() 元,試寫出利潤
元,試寫出利潤![]() 與銷售單價
與銷售單價![]() 之間的關系式;銷售單價為多少元時,可獲得最大利潤,最大利潤是多少元?
之間的關系式;銷售單價為多少元時,可獲得最大利潤,最大利潤是多少元?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
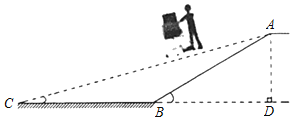
【題目】某商場為了方便消費者購物,準備將原來的階梯式自動扶梯改造成斜坡式自動扶梯.如圖所示,已知原階梯式扶梯AB長為10m,坡角∠ABD=30°;改造后斜坡式自動扶梯的坡角∠ACB=9°,請計算改造后的斜坡AC的長度,(結果精確到0.01(sin9°≈0.156,cos9°≈0.988,tan9°≈0.158)
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
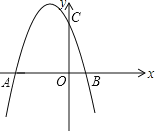
【題目】如圖,拋物線y=ax2+bx+3與x軸交于A(﹣3,0),B(l,0)兩點,與y軸交于點C.
(1)求拋物線的解析式;
(2)點P是拋物線上的動點,且滿足S△PAO=2S△PCO,求出P點的坐標;
(3)連接BC,點E是x軸一動點,點F是拋物線上一動點,若以B、C、E、F為頂點的四邊形是平行四邊形時,請直接寫出點F的坐標.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com