【題目】某中學開展“數學史”知識競賽活動，八年級（1）、（2）班根據初賽成績，各選出5名選手參加復賽，兩個班各選出的5名選手的復賽成績（滿分為100分）如圖所示．
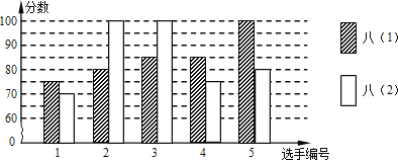
（1）請計算八（1）班、八（2）班兩個班選出的5名選手復賽的平均成績；
（2）請判斷哪個班選出的5名選手的復賽成績比較穩定，并說明理由？
【答案】（1）八（1）班和八（2）班兩個班選出的5名選手復賽的平均成績均為85分；（2）八（1）班的成績比較穩定，見解析
【解析】
（1）根據算術平均數的概念求解可得；
（2）先計算出兩個班的方差，再根據方差的意義求解可得．
（1）
=
（75+80+85+85+100）=85（分），
=（70+100+100+75+80）=85（分），
所以，八（1）班和八（2）班兩個班選出的5名選手復賽的平均成績均為85分．
（2）八（1）班的成績比較穩定．
理由如下：
s2八（1）=[（75-85）2+（80-85）2+（85-85）2+（85-85）2+（100-85）2]=70，
s2八（2）=[（70-85）2+（100-85）2+（100-85）2+（75-85）2+（80-85）2]=160，
∵s2八（1）＜s2八（2）
∴八（1）班的成績比較穩定．
科目：初中數學 來源： 題型：
【題目】如圖，拋物線y= 
x2+bx﹣2與x軸交于A、B兩點，與y軸交于C點，且A（﹣1，0）．
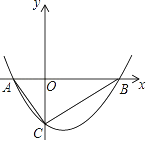
（1）求拋物線的解析式；
（2）判斷△ABC的形狀，證明你的結論．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在正方形ABCD中，AC為對角線，E為AB上一點，過點E作EF∥AD，與AC,DC分別交于點G，F，H為CG的中點，連接DE，EH，DH，FH．下列結論中結論正確的有（ ）
①EG=DF；
②∠AEH+∠ADH=180°；
③△EHF≌△DHC；
④若
，則S△EDH=13S△CFH .
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在圓心角為90°的扇形OAB中，點F、C在半徑OA、OB上，且OC=OF，以CF為邊作正方形CDEF，另兩頂點D、E在弧AB上，若扇形OAB的面積為25π，則正方形CDEF的面積為（ ）
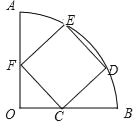
A. 25 B. 40 C. 50 D. 
π
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，∠ACB=90°，AC=15，BC=9，點P是線段AC上的一個動點，連接BP，將線段BP繞點P逆時針旋轉90°得到線段PD，連接AD，則線段AD的最小值是______．
查看答案和解析>>
科目：初中數學 來源： 題型：
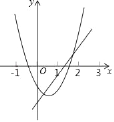
【題目】已知函數y=ax2+bx+c（a≠0）的圖象與函數y=x-
的圖象如圖所示，則下列結論：①ab>0；②c>-；③a+b+c<-
；④方程ax2+（b-1）x+c+=0有兩個不相等的實數根．其中正確的有( )
A. 4個 B. 3個 C. 2個 D. 1個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】一塊直角三角形的木板，它的一條直角邊AC長為1.5米，面積為1.5平方米.現在要把它加工成一個正方形桌面，甲、乙兩人的加工方法分別如圖(ⅰ)、(ⅱ)所示，記兩個正方形面積分別為S1、S2，請通過計算比較S1與S2的大小.
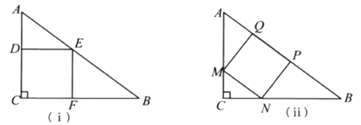
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】二次函數y＝ax2＋bx＋c的圖象如圖所示，對稱軸是直線x＝－1，有以下結論：①abc>0；②4ac<b2；③2a＋b＝0；④a－b＋c>0.其中正確的結論的個數是( )
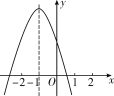
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某商人將進貨單價為
元的某種商品按
元銷售時，每天可賣出
件．現在他采用提高售價的辦法增加利潤，已知這種商品銷售單價每漲
元，銷售量就減少件，那么他將售價每個定為________元時，才能使每天所賺的利潤最大，每天最大利潤是________元．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com