
【題目】已知拋物線y=x2+bx+c經過點A(2,﹣3).
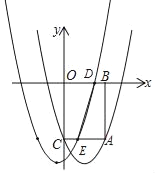
(1)如圖,過點A分別向x軸,y軸作垂線,垂足分別為B,C,得到矩形ABOC,且拋物線經過點C.
①求拋物線的解析式.
②將拋物線向左平移m(m>0)個單位,分別交線段OB,AC于D,E兩點.若直線DE剛好平分矩形ABOC的面積,求m的值.
(2)將拋物線平移,使點A的對應點為A1(2﹣n,3b),其中n≥1.若平移后的拋物線仍然經過點A,求平移后的拋物線頂點所能達到最高點時的坐標.

【答案】(1)①y=x2﹣2x﹣3;②m=![]() ;(2)頂點坐標(0,﹣7).
;(2)頂點坐標(0,﹣7).
【解析】
(1)①將A(2,﹣3),B(2,0)代入y=x2+bx+c即可求出;
②因為直線DE剛好平分矩形ABOC的面積,所以AE=OD=m,DB=CE=2﹣m,D(m,0),E(2﹣m,﹣3),易知F(3,0),所以DF=3﹣m,于是3﹣m=m,從而求出m;
(2)由拋物線y=x2+bx+c經過點A(2,﹣3),可得y=x2+bx﹣2b﹣7,由A的對應點為A1(2﹣n,3b),可知拋物線向左平移了n個單位,向上平移(3b+3)個單位,則平移后y=(x+n)2+b(x+n)﹣2b﹣7+3b+3,整理后根據平移后的拋物線仍然經過點A(2,﹣3),繼而可求得b=﹣n﹣1,進而可求得頂點坐標.
(1)①∵四邊形ABOC是矩形,A(2,﹣3),
∴B(2,0),C(0.﹣3),
∵拋物線y=x2+bx+c過點A、C,
∴![]() , 解得:
, 解得:![]() ,
,
∴拋物線解析式為y=x2﹣2x﹣3;
②如圖,設原拋物線與x軸正半軸交于點F,
∵直線DE剛好平分矩形ABOC的面積,
∴AE=OD=m,DB=CE=2﹣m
∴D(m,0),E(2﹣m,﹣3)
∵易知F(3,0),
∴DF=3﹣m,
∵DF=AE,
∴3﹣m=m,
∴m=![]() ;
;
(2)拋物線y=x2+bx+c經過點A(2,﹣3).
﹣3=22+2b+c,
∴c=﹣2b﹣7,
∴y=x2+bx﹣2b﹣7,
∵A的對應點為A1(2﹣n,3b),
∴拋物線向左平移了n個單位,向上平移(3b+3)個單位
則平移后y=(x+n)2+b(x+n)﹣2b﹣7+3b+3,
整理得y=(x+n)2+b(x+n)+b﹣4=(x+n+![]() )2﹣
)2﹣![]() +b﹣4,
+b﹣4,
∵平移后的拋物線仍然經過點A(2,﹣3),
∴﹣3=(2+n)2+b(2+n)+b﹣4,
∴n2+4n+3+b(3+n)=0,
∴(n+1(n+3))+b(n+3)=0,
(
∵n≥1,∴n+3>0,
∴n+1+b=0,b=﹣n﹣1,
頂點坐標(﹣n﹣![]() ,﹣
,﹣![]() +b﹣4),
+b﹣4),
y頂=﹣![]() +b﹣4=﹣
+b﹣4=﹣![]() (b﹣2)2﹣3=﹣
(b﹣2)2﹣3=﹣![]() (n+3)2﹣3,
(n+3)2﹣3,
∵n≥1,-![]() <0,
<0,
∴n=1時,頂點最高,此時b=﹣1﹣1=﹣2,
頂點坐標(0,﹣7).


科目:初中數學 來源: 題型:
【題目】定義:有一組對角互補的四邊形叫做互補四邊形.
![]() 概念理解:
概念理解:
①在互補四邊形![]() 中,
中,![]() 與
與![]() 是一組對角,若
是一組對角,若![]() 則
則![]() _
_ ![]()
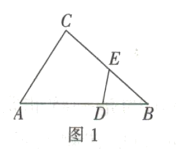
②如圖1,在![]() 中,點
中,點![]() 分別在邊
分別在邊![]() 上,且
上,且![]() 求證:四邊形
求證:四邊形![]() 是互補四邊形.
是互補四邊形.
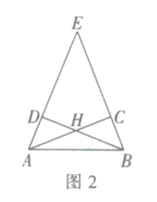
![]() 探究發現:如圖2,在等腰
探究發現:如圖2,在等腰![]() 中,
中,![]() 點
點![]() 分別在邊
分別在邊![]() 上,
上, ![]() 四邊形
四邊形![]() 是互補四邊形,求證:
是互補四邊形,求證:![]() .
.
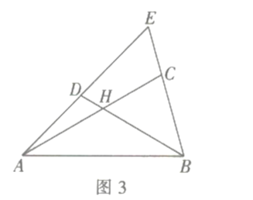
![]() 推廣運用:如圖3,在
推廣運用:如圖3,在![]() 中,點
中,點![]() 分別在邊
分別在邊![]() 上,
上,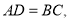 四邊形
四邊形![]() 是互補四邊形,若
是互補四邊形,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學開展以“我最喜歡的職業”為主題的調查活動,通過對學生的隨機抽樣調查得到一組數據,如圖是根據這組數據繪制成的不完整統計圖.
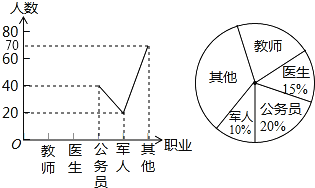
(1)把折線統計圖補充完整;
(2)求出扇形統計圖中,公務員部分對應的圓心角的度數;
(3)若從被調查的學生中任意抽取一名,求取出的這名學生最喜歡的職業是“教師”的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平直角坐標系中,規定:拋物線![]()
![]() 的相關直線為
的相關直線為![]() .例如:二次函數
.例如:二次函數![]() 的相關直線為
的相關直線為![]() .
.

(1)直接寫出拋物線![]() 的相關直線,并求出拋物線
的相關直線,并求出拋物線![]() 與其相關直線的交點坐標;
與其相關直線的交點坐標;
(2)如圖,拋物線![]()
![]() 與它的相關直線
與它的相關直線![]() 交于
交于![]() 、
、![]() 兩點.
兩點.
①求拋物線的解析式;
②連結![]() ,求
,求![]() 的面積;
的面積;
③作![]() ,過拋物線上一動點
,過拋物線上一動點![]() (不與
(不與![]() 、
、![]() 重合)作直線
重合)作直線![]() 的平行線交
的平行線交![]() 于點
于點![]() ,若以點
,若以點![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形是平行四邊形,直接寫出點
為頂點的四邊形是平行四邊形,直接寫出點![]() 的橫坐標.
的橫坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
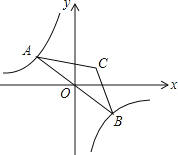
【題目】如圖,已知反比例函數y=﹣![]() 的圖象與直線y=kx(k<0)相交于點A、B,以AB為底作等腰三角形,使∠ACB=120°,且點C的位置隨著k的不同取值而發生變化,但點C始終在某一函數圖象上,則這個圖象所對應的函數解析式為__.
的圖象與直線y=kx(k<0)相交于點A、B,以AB為底作等腰三角形,使∠ACB=120°,且點C的位置隨著k的不同取值而發生變化,但點C始終在某一函數圖象上,則這個圖象所對應的函數解析式為__.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠有甲、乙兩臺機器加工同一種零件,已知一小時甲加工的零件數與一小時乙加工的零件數的和為36個,甲加工80個零件與乙加工100個零件的所用時間相等.求甲、乙兩臺機器每小時分別加工零件多少個?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() :
:![]() 與直線
與直線![]() 分別交于點
分別交于點![]() .直線
.直線![]() 與
與![]()
![]()
![]() 交于點
交于點![]() .記線段
.記線段![]() ,
,![]() 圍成的區域(不含邊界)為
圍成的區域(不含邊界)為![]() .橫,縱坐標都是整數的點叫做整點.
.橫,縱坐標都是整數的點叫做整點.
(1)當![]() 時,區域
時,區域![]() 內的整點個數為_____;
內的整點個數為_____;
(2)若區域![]() 內沒有整點,則
內沒有整點,則![]() 的取值范圍是_______.
的取值范圍是_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
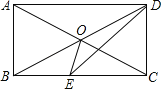
【題目】如圖,在四邊形ABCD中,AD∥BC,∠ABC=∠ADC,對角線AC、BD交于點O,AO=BO,DE平分∠ADC交BC于點E,連接OE.
(1)求證:四邊形ABCD是矩形;
(2)若AB=2,求△OEC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(問題)
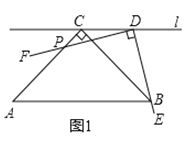
如圖1,在![]() 中,
中,![]() ,過點
,過點![]() 作直線
作直線![]() 平行于
平行于![]() .
.![]() ,點
,點![]() 在直線
在直線![]() 上移動,角的一邊
上移動,角的一邊![]() 始終經過點
始終經過點![]() ,另一邊
,另一邊![]() 與
與![]() 交于點
交于點![]() ,研究
,研究![]() 和
和![]() 的數量關系.
的數量關系.
(探究發現)
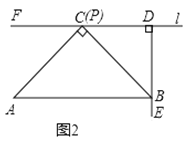
(1)如圖2,某數學興趣小組運用“從特殊到一般”的數學思想,發現當點![]() 移動到使點
移動到使點![]() 與點
與點![]() 重合時,通過推理就可以得到
重合時,通過推理就可以得到![]() ,請寫出證明過程;
,請寫出證明過程;
(數學思考)
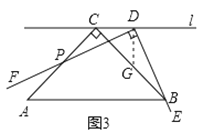
(2)如圖3,若點![]() 是
是![]() 上的任意一點(不含端點
上的任意一點(不含端點![]() ),受(1)的啟發,這個小組過點
),受(1)的啟發,這個小組過點![]() 作
作![]() 交
交![]() 于點
于點![]() ,就可以證明
,就可以證明![]() ,請完成證明過程;
,請完成證明過程;
(拓展引申)
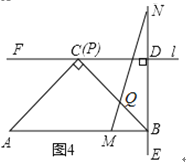
(3)如圖4,在(1)的條件下,![]() 是
是![]() 邊上任意一點(不含端點
邊上任意一點(不含端點![]() ),
),![]() 是射線
是射線![]() 上一點,且
上一點,且![]() ,連接
,連接![]() 與
與![]() 交于點
交于點![]() ,這個數學興趣小組經過多次取
,這個數學興趣小組經過多次取![]() 點反復進行實驗,發現點
點反復進行實驗,發現點![]() 在某一位置時
在某一位置時![]() 的值最大.若
的值最大.若![]() ,請你直接寫出
,請你直接寫出![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com