
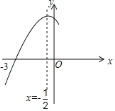
【題目】如圖,拋物線![]() 與
與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,其對(duì)稱(chēng)軸為直線
,其對(duì)稱(chēng)軸為直線![]() ,結(jié)合圖象分析下列結(jié)論:①
,結(jié)合圖象分析下列結(jié)論:①![]() ;②
;②![]() ;③當(dāng)
;③當(dāng)![]() 時(shí),
時(shí),![]() 隨
隨![]() 的增大而增大;④一元二次方程
的增大而增大;④一元二次方程![]() 的兩根分別為
的兩根分別為![]() ,
,![]() ;⑤
;⑤![]() ;⑥若
;⑥若![]() ,
,![]() 為方程
為方程![]() 的兩個(gè)根,則
的兩個(gè)根,則![]() 且
且![]() ,其中正確的結(jié)論有( )
,其中正確的結(jié)論有( )
A. ![]() 個(gè)B.
個(gè)B. ![]() 個(gè)C.
個(gè)C. ![]() 個(gè)D.
個(gè)D. ![]() 個(gè)
個(gè)
【答案】C
【解析】
利用二次函數(shù)圖象與系數(shù)的關(guān)系,結(jié)合圖象依次對(duì)各結(jié)論進(jìn)行判斷.
解:![]() 拋物線
拋物線![]() 與
與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,其對(duì)稱(chēng)軸為直線
,其對(duì)稱(chēng)軸為直線![]()
![]() 拋物線
拋物線![]() 與
與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() 和
和![]() ,且
,且![]()
由圖象知:![]() ,
,![]() ,
,![]()
![]()
![]()
故結(jié)論①正確;
![]() 拋物線
拋物線![]() 與x軸交于點(diǎn)
與x軸交于點(diǎn)![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
故結(jié)論②正確;
![]() 當(dāng)
當(dāng)![]() 時(shí),y隨x的增大而增大;當(dāng)
時(shí),y隨x的增大而增大;當(dāng)![]() 時(shí),
時(shí),![]() 隨
隨![]() 的增大而減小
的增大而減小
![]() 結(jié)論③錯(cuò)誤;
結(jié)論③錯(cuò)誤;
![]()
![]() ,
,![]()
![]()
![]()
![]() 拋物線
拋物線![]() 與
與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() 和
和![]()
![]()
![]() 的兩根是
的兩根是![]() 和
和![]()
![]()
![]() ,
,![]()
![]()
![]() 即為:
即為:![]() ,解得
,解得![]() ,
,![]() ;
;
故結(jié)論④正確;
![]() 當(dāng)
當(dāng)![]() 時(shí),
時(shí),![]()
![]()
![]()
故結(jié)論⑤正確;
![]() 拋物線
拋物線![]() 與
與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() 和
和![]() ,
,
![]()
![]()
![]()
![]() ,
,![]() 為方程
為方程![]() 的兩個(gè)根
的兩個(gè)根
![]()
![]() ,
,![]() 為方程
為方程![]() 的兩個(gè)根
的兩個(gè)根
![]()
![]() ,
,![]() 為函數(shù)
為函數(shù)![]() 與直線
與直線![]() 的兩個(gè)交點(diǎn)的橫坐標(biāo)
的兩個(gè)交點(diǎn)的橫坐標(biāo)
結(jié)合圖象得:![]() 且
且![]()
故結(jié)論⑥成立;
故選:C.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
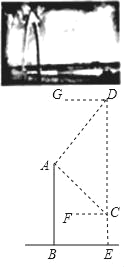
【題目】通達(dá)橋即小店汾河橋,是太原新建成的一座跨汾大橋,也是太原首座懸索橋.橋的主塔由曲線形拱門(mén)組成,取意“時(shí)代之門(mén)”.無(wú)人機(jī)社團(tuán)的同學(xué)計(jì)劃利用無(wú)人機(jī)設(shè)備測(cè)量通達(dá)橋拱門(mén)的高度.如圖,他們先將無(wú)人機(jī)升至距離橋面50米高的點(diǎn)C處,測(cè)得橋的拱門(mén)最高點(diǎn)A的仰角∠ACF為30°,再將無(wú)人機(jī)從C處豎直向上升高200米到點(diǎn)D處,測(cè)得點(diǎn)A的俯角∠ADG為45°.已知點(diǎn)A,B,C,D,E在同一平面內(nèi),求通達(dá)橋拱門(mén)最高點(diǎn)A距離橋面BE的高度AB.(結(jié)果保留整數(shù),參考數(shù)據(jù):![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
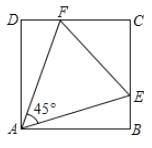
【題目】如圖,在正方形![]() 中,
中,![]() 、
、![]() 分別是邊
分別是邊![]() 、
、![]() 上的點(diǎn),
上的點(diǎn),![]() ,
,![]() 的周長(zhǎng)為6,則正方形
的周長(zhǎng)為6,則正方形![]() 的邊長(zhǎng)為__________.
的邊長(zhǎng)為__________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
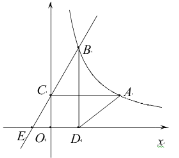
【題目】如圖,已知反比例函數(shù)![]() 的圖象經(jīng)過(guò)點(diǎn)
的圖象經(jīng)過(guò)點(diǎn)![]() ,過(guò)
,過(guò)![]() 作
作![]() 軸于點(diǎn)
軸于點(diǎn)![]() .點(diǎn)
.點(diǎn)![]() 為反比例函數(shù)圖象上的一動(dòng)點(diǎn),過(guò)點(diǎn)
為反比例函數(shù)圖象上的一動(dòng)點(diǎn),過(guò)點(diǎn)![]() 作
作![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,連接
,連接![]() .直線
.直線![]() 與
與![]() 軸的負(fù)半軸交于點(diǎn)
軸的負(fù)半軸交于點(diǎn)![]() .
.
(1)求反比例函數(shù)的表達(dá)式;
(2)若![]() ,求
,求![]() 的面積;
的面積;
(3)是否存在點(diǎn)![]() ,使得四邊形
,使得四邊形![]() 為平行四邊形?若存在,請(qǐng)求出點(diǎn)
為平行四邊形?若存在,請(qǐng)求出點(diǎn)![]() 的坐標(biāo);若不存在,請(qǐng)說(shuō)明理由.
的坐標(biāo);若不存在,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某班為參加學(xué)校的大課間活動(dòng)比賽,準(zhǔn)備購(gòu)進(jìn)一批跳繩,已知2根![]() 型跳繩和1根
型跳繩和1根![]() 型跳繩共需56元,1根
型跳繩共需56元,1根![]() 型跳繩和2根
型跳繩和2根![]() 型跳繩共需82元.
型跳繩共需82元.
(1)求一根![]() 型跳繩和一根
型跳繩和一根![]() 型跳繩的售價(jià)各是多少元?
型跳繩的售價(jià)各是多少元?
(2)學(xué)校準(zhǔn)備購(gòu)進(jìn)這兩種型號(hào)的跳繩共50根,并且![]() 型跳繩的數(shù)量不多于
型跳繩的數(shù)量不多于![]() 型跳繩數(shù)量的3倍,請(qǐng)?jiān)O(shè)計(jì)出最省錢(qián)的購(gòu)買(mǎi)方案,并說(shuō)明理由.
型跳繩數(shù)量的3倍,請(qǐng)?jiān)O(shè)計(jì)出最省錢(qián)的購(gòu)買(mǎi)方案,并說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某商店購(gòu)進(jìn)![]() 、
、![]() 兩種商品,購(gòu)買(mǎi)1個(gè)
兩種商品,購(gòu)買(mǎi)1個(gè)![]() 商品比購(gòu)買(mǎi)1個(gè)
商品比購(gòu)買(mǎi)1個(gè)![]() 商品多花10元,并且花費(fèi)300元購(gòu)買(mǎi)
商品多花10元,并且花費(fèi)300元購(gòu)買(mǎi)![]() 商品和花費(fèi)100元購(gòu)買(mǎi)
商品和花費(fèi)100元購(gòu)買(mǎi)![]() 商品的數(shù)量相等.
商品的數(shù)量相等.
(1)求購(gòu)買(mǎi)一個(gè)![]() 商品和一個(gè)
商品和一個(gè)![]() 商品各需要多少元;
商品各需要多少元;
(2)商店準(zhǔn)備購(gòu)買(mǎi)![]() 、
、![]() 兩種商品共80個(gè),若
兩種商品共80個(gè),若![]() 商品的數(shù)量不少于
商品的數(shù)量不少于![]() 商品數(shù)量的4倍,并且購(gòu)買(mǎi)
商品數(shù)量的4倍,并且購(gòu)買(mǎi)![]() 、
、![]() 商品的總費(fèi)用不低于1000元且不高于1050元,那么商店有哪幾種購(gòu)買(mǎi)方案?
商品的總費(fèi)用不低于1000元且不高于1050元,那么商店有哪幾種購(gòu)買(mǎi)方案?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖1,在平面直角坐標(biāo)系xOy中,半徑為1的⊙O與x軸正半軸和y軸正半軸分別交于A,B兩點(diǎn),直線l:y=kx+2(k<0)與x軸和y軸分別交于P,M兩點(diǎn).
(1)當(dāng)直線與⊙O相切時(shí),求出點(diǎn)M的坐標(biāo)和點(diǎn)P的坐標(biāo);
(2)如圖2,當(dāng)點(diǎn)P在線段OA上時(shí),直線1與⊙O交于E,F兩點(diǎn)(點(diǎn)E在點(diǎn)F的上方)過(guò)點(diǎn)F作FC∥x軸,與⊙O交于另一點(diǎn)C,連結(jié)EC交y軸于點(diǎn)D.
①如圖3,若點(diǎn)P與點(diǎn)A重合時(shí),求OD的長(zhǎng)并寫(xiě)出解答過(guò)程;
②如圖2,若點(diǎn)P與點(diǎn)A不重合時(shí),OD的長(zhǎng)是否發(fā)生變化,若不發(fā)生變化,請(qǐng)求出OD的長(zhǎng)并寫(xiě)出解答過(guò)程;若發(fā)生變化,請(qǐng)說(shuō)明理由.
(3)如圖4,在(2)的基礎(chǔ)上,連結(jié)BF,將線段BF繞點(diǎn)B逆時(shí)針旋轉(zhuǎn)90°到BQ,若點(diǎn)Q在CE的延長(zhǎng)線時(shí),請(qǐng)用等式直接表示線段FC,FQ之間的數(shù)量關(guān)系.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖①所示,已知正方形ABCD和正方形AEFG,連接DG,BE.
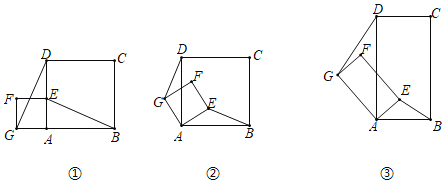
(1)發(fā)現(xiàn):當(dāng)正方形AEFG繞點(diǎn)A旋轉(zhuǎn),如圖②所示.
①線段DG與BE之間的數(shù)量關(guān)系是 ;
②直線DG與直線BE之間的位置關(guān)系是 ;
(2)探究:如圖③所示,若四邊形ABCD與四邊形AEFG都為矩形,且AD=2AB,AG=2AE時(shí),上述結(jié)論是否成立,并說(shuō)明理由.
(3)應(yīng)用:在(2)的情況下,連接BG、DE,若AE=1,AB=2,求BG2+DE2的值(直接寫(xiě)出結(jié)果).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】(6分)如圖,菱形ABCD的對(duì)角線AC,BD相交于點(diǎn)O,分別延長(zhǎng)OA,OC到點(diǎn)E,F,使AE=CF,依次連接B,F,D,E各點(diǎn).

(1)求證:△BAE≌△BCF;
(2)若∠ABC=50°,則當(dāng)∠EBA= °時(shí),四邊形BFDE是正方形.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com