
【題目】某新建成學校舉行美化綠化校園活動,九年級計劃購買![]() ,
,![]() 兩種花木共100棵綠化操場,其中
兩種花木共100棵綠化操場,其中![]() 花木每棵50元,
花木每棵50元,![]() 花木每棵100元.
花木每棵100元.
(1)若購進![]() ,
,![]() 兩種花木剛好用去8000元,則購買了
兩種花木剛好用去8000元,則購買了![]() 兩種花木各多少棵?
兩種花木各多少棵?
(2)如果購買![]() 花木的數量不少于
花木的數量不少于![]() 花木的數量,請設計一種購買方案使所需總費用最低,并求出該購買方案所需總費用?
花木的數量,請設計一種購買方案使所需總費用最低,并求出該購買方案所需總費用?
【答案】(1)購買A種花木40棵,B種花木60棵;(2)當購買A種花木50棵、B種花木50棵時,所需總費用最低,最低費用為7500元.
【解析】
試題分析:(1)設購買A種花木x棵,B種花木y棵,根據“A,B兩種花木共100棵、購進A,B兩種花木剛好用去8000元”列方程組求解可得;
(2)設購買A種花木a棵,則購買B種花木(100﹣a)棵,根據“B花木的數量不少于A花木的數量”求得a的范圍,再設購買總費用為W,列出W關于a的解析式,利用一次函數的性質求解可得.
試題解析:(1)設購買A種花木x棵,B種花木y棵,
根據題意,得:![]() ,解得:
,解得:![]() ,
,
答:購買A種花木40棵,B種花木60棵;
(2)設購買A種花木a棵,則購買B種花木(100﹣a)棵,
根據題意,得:100﹣a≥a,解得:a≤50,
設購買總費用為W,則W=50a+100(100﹣a)=﹣50a+10000,
∵W隨a的增大而減小,∴當a=50時,W取得最小值,最小值為7500元,
答:當購買A種花木50棵、B種花木50棵時,所需總費用最低,最低費用為7500元.


 小博士期末闖關100分系列答案
小博士期末闖關100分系列答案 名校名師培優作業本加核心試卷系列答案
名校名師培優作業本加核心試卷系列答案科目:初中數學 來源: 題型:
【題目】甲、乙兩運動員的射擊成績(靶心為10環)統計如下表(不完全):
次數 運動員 環數 | 1 | 2 | 3 | 4 | 5 |
甲 | 10 | 8 | 9 | 10 | 8 |
乙 | 10 | 9 | 9 | a | b |
某同學計算出了甲的成績平均數是9,方差是![]() ,請作答:
,請作答:
(1)在圖中用折線統計圖將甲運動員的成績表示出來;
(2)若甲、乙的射擊成績平均數都一樣,則![]() ;
;
(3)在(2)的條件下,當甲比乙的成績較穩定時,請列舉出![]() 的所有可能取值,并說明理由.
的所有可能取值,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,△ABC的三個頂點分別為A(﹣1,﹣2),B(﹣2,﹣4),C(﹣4,﹣1).
(1)把△ABC向上平移3個單位后得到△A1B1C1,請畫出△A1B1C1并寫出點B1的坐標;
(2)已知點A與點A2(2,1)關于直線l成軸對稱,請畫出直線l及△ABC關于直線l對稱的△A2B2C2,并直接寫出直線l的函數解析式.
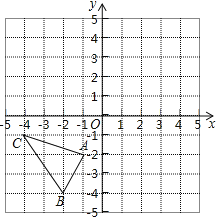
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一次體育達標測試中,九年級(2)班15名男生的引體向上成績如下表:問這15名男生的引體向上成績的中位數和眾數分別是( )
成績/個 | 8 | 9 | 11 | 12 | 13 | 15 |
人數 | 1 | 2 | 3 | 4 | 3 | 2 |
A.12,13B.12,12C.11,12D.3,4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖甲,直線y=﹣x+3與x軸、y軸分別交于點B、點C,經過B、C兩點的拋物線y=x2+bx+c與x軸的另一個交點為A,頂點為P.
(1)求該拋物線的解析式;
(2)在該拋物線的對稱軸上是否存在點M,使以C,P,M為頂點的三角形為等腰三角形?若存在,請直接寫出所符合條件的點M的坐標;若不存在,請說明理由;
(3)當0<x<3時,在拋物線上求一點E,使△CBE的面積有最大值(圖乙、丙供畫圖探究).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】新冠狀病毒疫情發生以來,截止2月5日全國紅十字會共接收社會捐贈款物約6.5993×109元.數據6.5993×109可以表示為( )
A.0.65993億B.6.5993億C.65.993億D.659.93億
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】新農村社區改造中,有一部分樓盤要對外銷售,某樓盤共23層,銷售價格如下:第八層樓房售價為4000元/米2 , 從第八層起每上升一層,每平方米的售價提高50元;反之,樓層每下降一層,每平方米的售價降低30元,已知該樓盤每套樓房面積均為120米2 . 若購買者一次性付清所有房款,開發商有兩種優惠方案:
方案一:降價8%,另外每套樓房贈送a元裝修基金;
方案二:降價10%,沒有其他贈送.
(1)請寫出售價y(元/米2)與樓層x(1≤x≤23,x取整數)之間的函數關系式;
(2)老王要購買第十六層的一套樓房,若他一次性付清購房款,請幫他計算哪種優惠方案更加合算.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com