
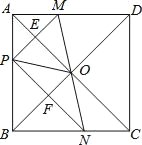
【題目】如圖,在正方形![]() 中,點
中,點![]() 是
是![]() 上一動點(不與
上一動點(不與![]() ,
,![]() 重合),對角線
重合),對角線![]() 、
、![]() 相交于點
相交于點![]() ,過點
,過點![]() 分別作
分別作![]() 、
、![]() 的垂線,分別交
的垂線,分別交![]() 、
、![]() 于點
于點![]() 、
、![]() ,交
,交![]() 、
、![]() 于點
于點![]() 、
、![]() .下列結論:①
.下列結論:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤當
;⑤當![]() 時,點
時,點![]() 是
是![]() 的中點.
的中點.
其中正確的結論有_____.
【答案】①②③⑤
【解析】
①根據正方形的每一條對角線平分一組對角可得∠PAE=∠MAE=45°,然后利用“角邊角”證明△APE和△AME全等;
②根據全等三角形對應邊相等可得PE=EM=![]() PM,同理,FP=FN=
PM,同理,FP=FN=![]() NP,證出四邊形PEOF是矩形,得出PF=OE,證得△APE為等腰直角三角形,得出AE=PE,PE+PF=OA,即可得到PM+PN=AC;
NP,證出四邊形PEOF是矩形,得出PF=OE,證得△APE為等腰直角三角形,得出AE=PE,PE+PF=OA,即可得到PM+PN=AC;
③根據矩形的性質可得PF=OE,再利用勾股定理即可得到PE2+PF2=PO2;
④判斷出△POF不一定等腰直角三角形,△BNF是等腰直角三角形,從而確定出兩三角形不一定相似;
⑤證出△APM和△BPN以及△APE、△BPF都是等腰直角三角形,從而得出結論.
解:①∵四邊形![]() 是正方形,
是正方形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
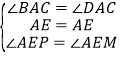 ,
,
∴![]() ,
,
故①正確;
②∵![]() ,
,
∴![]() ,
,
同理,![]() ,
,
∵正方形![]() 中,
中,![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ,且
,且![]() 中
中![]() ,
,
∴四邊形![]() 是矩形.
是矩形.
∴![]() ,
,
∵在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() 為等腰直角三角形,
為等腰直角三角形,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
故②正確;
③∵四邊形![]() 是矩形,
是矩形,
∴![]() ,
,
在直角![]() 中,
中,![]() ,
,
∴![]() ,
,
故③正確;
④∵![]() ,
,
∴![]() .
.
![]() 是等腰直角三角形,而
是等腰直角三角形,而![]() 不一定是,
不一定是,
∴![]() 與
與![]() 不一定相似,
不一定相似,
故④錯誤;
⑤∵![]() ,
,
∴![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
同理,![]() 是等腰直角三角形,
是等腰直角三角形,
當![]() 時,
時,![]() 是等腰直角三角形.
是等腰直角三角形.
∴![]() ,
,
又∵![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,
∴![]() ,即
,即![]() 是
是![]() 的中點,
的中點,
故⑤正確;
故答案為:①②③⑤.


 天天練口算系列答案
天天練口算系列答案科目:初中數學 來源: 題型:
【題目】已知關于x的一元二次方程ax2+x+2=0.
(1)求證:當a<0時,方程ax2+x+2=0一定有兩個不等的實數根;
(2)若代數式﹣x2+x+2的值為正整數,且x為整數時,求x的值;
(3)當a=a1時,拋物線y=ax2+x+2與x軸的正半軸相交于點M(m,0);當a=a2時,拋物線y=ax2+x+2與x軸的正半軸相交于點N(n,0);若點M在點N的左邊,試比較a1與a2的大小.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現如今,“垃圾分類”意識已深入人心,垃圾一般可分為:可回收物、廚余垃圾、有害垃圾、其它垃圾.其中甲拿了一袋垃圾,乙拿了兩袋垃圾.
(1)直接寫出甲所拿的垃圾恰好是“廚余垃圾”的概率;
(2)求乙所拿的兩袋垃圾不同類的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
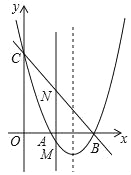
【題目】如圖,拋物線y=x2+bx+c與x軸交于點A和B(3,0),與y軸交于點C(0,3).
(1)求拋物線的解析式;
(2)若點M是拋物線上在x軸下方的動點,過M作MN∥y軸交直線BC于點N,求線段MN的最大值;
(3)E是拋物線對稱軸上一點,F是拋物線上一點,是否存在以A,B,E,F為頂點的四邊形是平行四邊形?若存在,請直接寫出點F的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】怡然美食店的A、B兩種菜品,每份成本均為14元,售價分別為20元、18元,這兩種菜品每天的營業額共為1120元,總利潤為280元.
(1)該店每天賣出這兩種菜品共多少份?
(2)該店為了增加利潤,準備降低A種菜品的售價,同時提高B種菜品的售價,售賣時發現,A種菜品售價每降0.5元可多賣1份;B種菜品售價每提高0.5元就少賣1份,如果這兩種菜品每天銷售總份數不變,那么這兩種菜品一天的總利潤最多是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】今年“五一”節,小明外出爬山,他從山腳爬到山頂的過程中,中途休息了一段時間.設他從山腳出發后所用時間為t(分鐘),所走路程為s(米),s與t之間的函數關系如圖所示,則下列說法中,錯誤的是( )
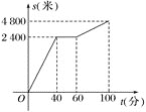
A. 小明中途休息用了20分鐘 B. 小明休息前爬山的速度為每分鐘60米
C. 小明在上述過程中所走路程為7 200米 D. 小明休息前后爬山的平均速度相等
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知A(﹣2,0),B(4,0),拋物線y=ax2+bx﹣1過A、B兩點,并與過A點的直線y=﹣![]() x﹣1交于點C.
x﹣1交于點C.
(1)求拋物線解析式及對稱軸;
(2)在拋物線的對稱軸上是否存在一點P,使四邊形ACPO的周長最小?若存在,求出點P的坐標,若不存在,請說明理由;
(3)點M為y軸右側拋物線上一點,過點M作直線AC的垂線,垂足為N.問:是否存在這樣的點N,使以點M、N、C為頂點的三角形與△AOC相似,若存在,求出點N的坐標,若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,河的兩岸l1與l2相互平行,A、B是l1上的兩點,C、D是l2上的兩點,某人在點A處測得∠CAB=90°,∠DAB=30°,再沿AB方向前進20米到達點E(點E在線段AB上),測得∠DEB=60°,求C、D兩點間的距離.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨若移動終端設備的升級換代,手機已經成為我們生活中不可缺少的一部分,為了解中學生在假期使用手機的情況(選項:A .和同學親友聊天;B.學習;C.購物;D.游戲;E.其它),端午節后某中學在全校范圍內隨機抽取了若干名學生進行調査,得到如下圖表(部分信息未給出):

根據以上信息解答下列問題:
(1)這次被調查的學生有多少人?
(2)求表中![]() 的值,并補全條形統計圖;
的值,并補全條形統計圖;
(3)若該中學約有![]() 名學生,估計全校學生中利用手機購物或玩游戲的共有多少人?
名學生,估計全校學生中利用手機購物或玩游戲的共有多少人?
并根據以上調査結果,就中學生如何合理使用手機給出你的一條建議.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com