
【題目】某校九年級甲、乙兩班各有學生50人,為了了解這兩個班學生身體素質情況,進行了抽樣調查,數據整理過程如下,請完成下面數據整理中的問題:
(1)收集數據
從甲、乙兩個班中各隨機抽取10名學生進行身體素質測試,測試成績(百分制)如下:
甲班:65,75,75,80,60,50,75,90,85,65;
乙班:90,55,80,70,55,70,95,80,65,70;
(2)整理描述數據
按如下分數段整理、描述這兩組樣本數據:
成績x 人數 班級 | 50≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x<100 |
甲班 | 1 | 3 | 3 | 2 | 1 |
乙班 | 2 | 1 | m | 2 | n |
在表中:m= ,n= ;
(3)分析數據
①若規定測試成績在80分(含80分)以上的學生身體素質為優秀,請估計乙班50名學生中身體素質為優秀的學生有 人;
②現從甲班指定的3名學生(1男2女),乙班指定的2名學生(1男1女)中分別抽取1名學生去參加身體素質拓展訓練,用樹狀圖或列表法求出抽到的2名同學中恰好是1男1女的概率.
 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中數學 來源: 題型:
【題目】如圖,以AB邊為直徑的⊙O經過點P,C是⊙O上一點,連結PC交AB于點E,且∠ACP=60°,PA=PD.
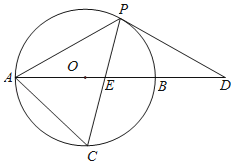
(1)試判斷PD與⊙O的位置關系,并說明理由;
(2)若點C是弧AB的中點,已知AB=2,求CECP的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩個袋中均裝有三張除所標數值外完全相同的卡片,甲袋中的三張卡片上所標有的三個數值為﹣7,﹣1,3.乙袋中的三張卡片所標的數值為﹣2,1,6.先從甲袋中隨機取出一張卡片,用x表示取出的卡片上的數值,再從乙袋中隨機取出一張卡片,用y表示取出卡片上的數值,把x、y分別作為點A的橫坐標和縱坐標.
(1)用適當的方法寫出點A(x,y)的所有情況.
(2)求點A落在第三象限的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
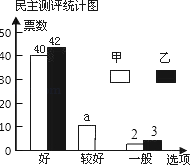
【題目】在校園歌手大賽中,甲、乙兩位同學的表現分外突出,現場A、B、C、D、E、F六位評委的打分情況以及隨機抽取的50名同學的民意調查結果分別如下統計表和不完整的條形統計圖:(說明:隨機抽取的50名同學每人必須從“好”、“較好”、“一般”中選一票投給每個選手)
A | B | C | D | E | F | |
甲 | 89 | 97 | 90 | 93 | 95 | 94 |
乙 | 89 | 92 | 90 | 97 | 94 | 94 |
(1)a= ,六位評委對乙同學所打分數的中位數是 ,并補全條形統計圖;
(2)學校規定評分標準如下:去掉評委評分中最高和最低分,再算平均分并將平均分與民意測評分按2:3計算最后得分.求甲、乙兩位同學的最后得分.(民意測評分=“好”票數×2+“較好”票數×1+“一般”票數×0)
查看答案和解析>>
科目:初中數學 來源: 題型:
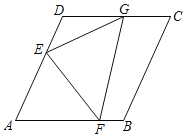
【題目】如圖在菱形紙片ABCD中,AB=4,∠B=120°,將菱形紙片翻折,使點A落在邊CD的中點G處,折痕為EF,點E,F分別在邊AD,AB上,則sin∠GEF的值為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是拋物線![]() 圖像的一部分,拋物線的項點坐標是A(1,3),與
圖像的一部分,拋物線的項點坐標是A(1,3),與![]() 軸的一個交點B(4,0),直線
軸的一個交點B(4,0),直線![]() 與拋物線交于
與拋物線交于![]() ,
,![]() 兩點,下列結論:①
兩點,下列結論:①![]() :②
:②![]()
![]() ;③方程
;③方程![]() 有兩個相等的實數根:④當
有兩個相等的實數根:④當![]() 時,有
時,有![]() ;⑤拋物線與
;⑤拋物線與![]() 軸的另一個交點是(-1,0),其中正確的是( )
軸的另一個交點是(-1,0),其中正確的是( )

A.①②③B.①③④C.①③⑤D.②④⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
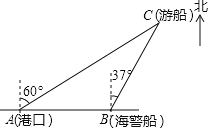
【題目】一艘觀光游船從港口A以北偏東60°的方向出港觀光,航行80海里至C處時發生了側翻沉船事故,立即發出了求救信號,一艘在港口正東方向的海警船接到求救信號,測得事故船在它的北偏東37°方向,馬上以40海里每小時的速度前往救援,
(1)求點C到直線AB的距離;
(2)求海警船到達事故船C處所需的大約時間.(溫馨提示:sin53°≈0.8,cos53°≈0.6)
查看答案和解析>>
科目:初中數學 來源: 題型:
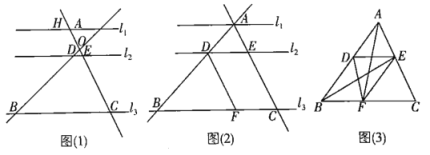
【題目】如圖(1),![]() ,直線AB和CH交于點O,分別交
,直線AB和CH交于點O,分別交![]() 于D、E兩點,已知
于D、E兩點,已知![]() ,
,![]() ,
,![]() .
.
(1)嘗試探究:在圖(1)中,求DB和AD的長;
(2)類比延伸:平移AB使得A與H重合,如圖(2)所示,過點D作![]() ,若
,若![]() ,求線段BF的長;
,求線段BF的長;
(3)拓展遷移:如圖(3),若![]() 的面積是10,點D、E分別位于AB、CA上,
的面積是10,點D、E分別位于AB、CA上,![]() ,點F在BC上且
,點F在BC上且![]() ,
,![]() ,如果
,如果![]() 的面積和四邊形FCED的面積相等,求這個相等的面積.
的面積和四邊形FCED的面積相等,求這個相等的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】《九章算術》是中國傳統數學最重要的著作,奠定了中國傳統數學的基本框架.它的代數成就主要包括開方術、正負術和方程術.其中,方程術是《九章算術》最高的數學成就.《九章算術》“勾股”一章記載:“今有戶高多于廣六尺八寸,兩隅相去適一丈.問戶高、廣各幾何?”譯文:已知長方形門的高比寬多6尺8寸,門的對角線長1丈,那么門的高和寬各是多少?(1丈=10尺,1尺=10寸)設長方形門的寬![]() 尺,可列方程為_______.
尺,可列方程為_______.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com