【題目】如果a是一個三位數，現在把1放在它的右邊，得到一個四位數，這個四位數是（ ）
A. 1000a+1 B. 100a+1 C. 10a+1 D. a+1
天天向上口算本系列答案科目：初中數學 來源： 題型：
【題目】如圖，小敏做了一個角平分儀ABCD，其中AB=AD，BC=DC．將儀器上的點A與∠PRQ的頂點R重合，調整AB和AD，使它們分別落在角的兩邊上，過點A，C畫一條射線AE，AE就是∠PRQ的平分線．此角平分儀的畫圖原理是：根據儀器結構，可得△ABC≌△ADC，這樣就有∠QAE=∠PAE．則說明這兩個三角形全等的依據是（ ）
A．SAS B．ASA C．AAS D．SSS
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下列說法:①兩點之間的所有連線中，線段最短；②兩點之間的距離是兩點間的線段；③過直線外一點有且僅有一條直線與己知直線平行；④相等的角是對頂角.其中正確的個數是( )
A. 1個 B. 2個 C. 3個 D .4個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某市“藝術節”期間，小明、小亮都想去觀看茶藝表演，但是只有一張茶藝表演門票，他們決定采用抽卡片的辦法確定誰去．規則如下：
將正面分別標有數字1、2、3、4的四張卡片（除數字外其余都相同）洗勻后，背面朝上放置在桌面上，隨機抽出一張記下數字后放回；重新洗勻后背面朝上放置在桌面上，再隨機抽出一張記下數字．如果兩個數字之和為奇數，則小明去；如果兩個數字之和為偶數，則小亮去．
（1）請用列表或畫樹狀圖的方法表示抽出的兩張卡片上的數字之和的所有可能出現的結果；
（2）你認為這個規則公平嗎？請說明理由．
考點：游戲公平性；列表法與樹狀圖法．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（本題8分）如下圖，在每個小正方形邊長為1的方格紙中，△ABC的頂點都在方格紙格點上．
（1）△ABC的面積為 ；
（2）將△ABC經過平移后得到△A′B′C′，圖中標出了點B的對應點B'，補全△A′B′C′；
（3）在圖中畫出△ABC的高CD；
（4）若連接
， 
，則這兩條線段之間的關系是 ；
（5）能使S△ABC＝S△QBC的格點Q，共有 個．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了豐富群眾文化生活，某縣城區已經整體轉換成了數字電視．目前該縣廣播電視信息網絡公司正在對鄉鎮進行數字電視改裝．公司現有400戶申請了但還未安裝的用戶，此外每天還有新的用戶申請．已知每個安裝小組每天安裝的數量相同，且每天申請安裝的用戶數也相同，公司若安排3個安裝小組同時安裝，則50天可以安裝完所有新、舊申請用戶；若公司安排5個安裝小組同時安裝，則10天可以安裝完所有新，舊申請用戶．
（1）求每天新申請安裝的用戶數及每個安裝小組每天安裝的數量；
（2）如果要求在8天內安裝完所有新、舊申請用戶，但前3天只能派出2個安裝小組安裝，那么最后幾天至少需要增加多少個安裝小組同時安裝，才能完成任務？
查看答案和解析>>
科目：初中數學 來源： 題型：
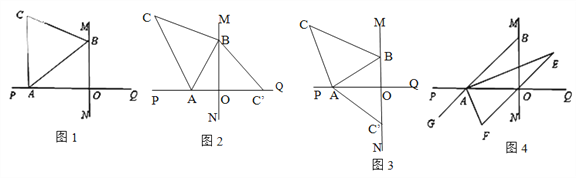
【題目】直線MN與直線PQ垂直相交于O，點A在射線OP上運動，點B 在射線OM上運動,A、B不與點O重合，如圖1，已知AC、BC分別是∠BAP和∠ABM角的平分線，
（1）點A、B在運動的過程中，∠ACB的大小是否發生變化？若發生變化，請說明理由；若不發生變化，試求出∠ACB的大小.
（2）如圖2，將△ABC沿直線AB折疊，若點C落在直線PQ上，則∠ABO＝________,
如圖3，將△ABC沿直線AB折疊，若點C落在直線MN上，則∠ABO＝________
（3）如圖4，延長BA至G，已知∠BAO、∠OAG的角平分線與∠BOQ的角平分線及其延長線交于E、F，則∠EAF＝ ；在△AEF中，如果有一個角是另一個角的
倍，求∠ABO的度數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
