
【題目】如圖,在△ABC中,點E在AC上,∠AEB=∠ABC.
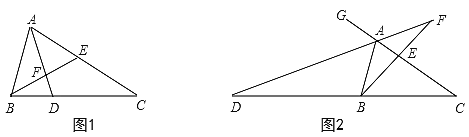
(1)圖1中,作∠BAC的角平分線AD,分別交CB、BE于D、F兩點,求證:∠EFD=∠ADC;
(2)圖2中,作△ABC的外角∠BAG的角平分線AD,分別交CB、BE的延長線于D、F兩點,試探究(1)中結論是否仍成立?為什么?
【答案】(1)證明見解析;(2)(1)中結論仍成立,理由見解析.
【解析】
(1)首先根據角平分線的性質可得∠BAD=∠DAC,再根據內角與外角的性質可得∠EFD=∠DAC+∠AEB,∠ADC=∠ABC+∠BAD,進而得到∠EFD=∠ADC;
(2)首先根據角平分線的性質可得∠BAD=∠DAG,再根據等量代換可得∠FAE=∠BAD,然后再根據內角與外角的性質可得∠EFD=∠AEB-∠FAE,∠ADC=∠ABC-∠BAD,進而得∠EFD=∠ADC.
(1)∵AD平分∠BAC,
∴∠BAD=∠DAC,
∵∠EFD=∠DAC+∠AEB,∠ADC=∠ABC+∠BAD,
又∵∠AEB=∠ABC,
∴∠EFD=∠ADC;
(2)探究(1)中結論仍成立;理由:
∵AD平分∠BAG,
∴∠BAD=∠GAD,
∵∠FAE=∠GAD,
∴∠FAE=∠BAD,
∵∠EFD=∠AEB-∠FAE,∠ADC=∠ABC-∠BAD,
又∵∠AEB=∠ABC,
∴∠EFD=∠ADC.


科目:初中數學 來源: 題型:
【題目】如圖,二次函數y=ax2+bx+c的圖象開口向上,對稱軸為直線x=1,圖象經過(3,0),下列結論中,正確的一項是( ) 
A.abc<0
B.2a+b<0
C.a﹣b+c<0
D.4ac﹣b2<0
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某廠生產橫截面直徑為7cm的圓柱形罐頭盒,需將“蘑菇罐頭”字樣貼在罐頭側面.為了獲得較佳視覺效果,字樣在罐頭盒側面所形成的弧的度數為90°,則“蘑菇罐頭”字樣的長度為( ) 
A.![]() cm
cm
B.![]() cm
cm
C.![]() cm
cm
D.7πcm
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,把△ABC紙片沿DE折疊,當點A落在四邊形BCDE內時,∠A與∠1+∠2之間有始終不變的關系是( )

A. ∠A=∠1+∠2 B. 2∠A=∠1+∠2 C. 3∠A=∠1+∠2 D. 3∠A=2(∠1+∠2)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=kx+1(k≠0)與反比例函數y= ![]() (m≠0)的圖象有公共點A(1,2).直線l⊥x軸于點N(3,0),與一次函數和反比例函數的圖象分別交于點B,C.
(m≠0)的圖象有公共點A(1,2).直線l⊥x軸于點N(3,0),與一次函數和反比例函數的圖象分別交于點B,C. 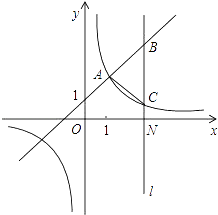
(1)求一次函數與反比例函數的解析式;
(2)求△ABC的面積?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某鎮水庫的可用水量為12000萬立方米,假設年降水量不變,能維持該鎮16萬人20年的用水量.實施城市化建設,新遷入4萬人后,水庫只夠維持居民15年的用水量.
(1)問:年降水量為多少萬立方米?每人年平均用水量多少立方米?
(2)政府號召節約用水,希望將水庫的保用年限提高到25年,則該鎮居民人均每年需節約多少立方米才能實現目標?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某省是勞務輸出大省,農民外出務工增長家庭收入的同時,也一定程度影響了子女的管理和教育,缺少管理和教育的留守兒童的學習和心理健康狀況等問題日趨顯現,成為社會關注的焦點.該省相關部門就留守兒童學習和心理健康狀況等問題進行調查,本次抽樣調查了該省某縣部分留守兒童,將調查出現的情況分四類,即A類:基本情況正常;B類;有輕度問題;C類:有較為嚴重問題;D類:有特別嚴重問題.通過調查,得到下面兩幅不完整的統計圖,請根據圖中的信息解決下面的問題. 
(1)在這次隨機抽樣調查中,共抽查了多少名學生留守兒童?
(2)扇形統計圖中C類所占的圓心角是°;這次調查中為D類的留守兒童有人;
(3)請你估計該縣20000名留守兒童中,出現較為嚴重問題及以上的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在四邊形ABCD中,∠DAB被對角線AC平分,且AC2=ABAD.我們稱該四邊形為“可分四邊形”,∠DAB稱為“可分角”.
(1)如圖2,在四邊形ABCD中,∠DAB=60°,AC平分∠DAB,且∠BCD=150°,求證:四邊形ABCD為“可分四邊形”;
(2)如圖3,四邊形ABCD為“可分四邊形”,∠DAB為“可分角”,如果∠DCB=∠DAB,則求∠DAB的度數;
(3)現有四邊形ABCD為“可分四邊形”,∠DAB為“可分角”,且AC=4,則△DAB的最大面積等于 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某班有50位學生,每位學生都有一個序號,將50張編有學生序號(從1號到50號)的卡片(除序號不同外其它均相同)打亂順序重新排列,從中任意抽取1張卡片.
(1)在序號中,是20的倍數的有:20,40,能整除20的有:1,2,4,5,10(為了不重復計數,20只計一次),求取到的卡片上序號是20的倍數或能整除20的概率;
(2)若規定:取到的卡片上序號是k(k是滿足1≤k≤50的整數),則序號是k的倍數或能整除k(不重復計數)的學生能參加某項活動,這一規定是否公平?請說明理由;
(3)請你設計一個規定,能公平地選出10位學生參加某項活動,并說明你的規定是符合要求的.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com