
【題目】如圖.已知A、B兩點的坐標分別為A(0,![]() ),B(2,0).直線AB與反比例函數(shù)
),B(2,0).直線AB與反比例函數(shù)![]() 的圖象交于點C和點D(
的圖象交于點C和點D(![]() 1,a).
1,a).
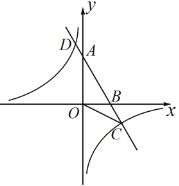
(1)求直線AB和反比例函數(shù)的解析式.
(2)求∠ACO的度數(shù).
【答案】(1)y=![]() x+
x+![]() ,y=﹣
,y=﹣![]() ;(2)∠ACO=30°;
;(2)∠ACO=30°;
【解析】
(1)根據(jù)A、B兩點坐標求得一次函數(shù)解析式,再求得D點的具體坐標,從而求得反比例函數(shù)的解析式.
(2)聯(lián)立函數(shù)解析式求得C點坐標,過C點作CH⊥x軸于H,證明![]() 為等腰三角形,根據(jù)特殊直角三角形求得
為等腰三角形,根據(jù)特殊直角三角形求得![]() 的度數(shù),從而求得
的度數(shù),從而求得![]() 的度數(shù).
的度數(shù).
解:(1)設直線AB的解析式為:![]() ,
,
把A(0,![]() ),B(2,0)分別代入,
),B(2,0)分別代入,
得,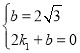 ,
,
解得![]() =
=![]() ,b=
,b=![]() .
.
∴直線AB的解析式為:y=![]() x+
x+![]() ;
;
∵點D(![]() 1,a)在直線AB上,
1,a)在直線AB上,
∴a=![]() +
+![]() =
=![]() ,即D點坐標為(
,即D點坐標為(![]() 1,
1,![]() ),
),
又∵D點(![]() 1,
1,![]() )在反比例函數(shù)
)在反比例函數(shù)![]() 的圖象上,
的圖象上,
∴k=![]() 1×
1×![]() =﹣
=﹣![]() ,
,
∴反比例函數(shù)的解析式為:y=﹣![]() ;
;
(2)由 ,解得
,解得 或
或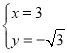 ,
,
∴C點坐標為(3,﹣![]() ),過C點作CH⊥x軸于H,如圖,
),過C點作CH⊥x軸于H,如圖,
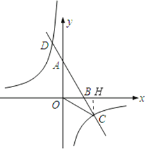
∵OH=3,CH=![]() ,
,
∴OC=![]() ,而OA=
,而OA=![]() ,
,
∴OA=OC,
∴∠OAC=∠OCA.
又∵OB=2,
∴AB=![]() ,
,
在Rt△AOB中,
∴∠OAB=30°,
∴∠ACO=30°


 靈星計算小達人系列答案
靈星計算小達人系列答案 孟建平錯題本系列答案
孟建平錯題本系列答案科目:初中數(shù)學 來源: 題型:
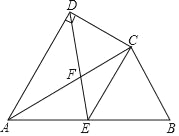
【題目】如圖,在四邊形ABCD中,AC平分∠DAB,AC2=ABAD,∠ADC=90°,點E為AB的中點.
(1)求證:△ADC∽△ACB.
(2)若AD=2,AB=3,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,矩形ABCD的兩邊長AB=18cm,AD=4cm,點P、Q分別從A、B同時出發(fā),P在邊AB上沿AB方向以每秒2cm的速度勻速運動,Q在邊BC上沿BC方向以每秒1cm的速度勻速運動.設運動時間為x秒,△PBQ的面積為y(cm2).
(1)求y關(guān)于x的函數(shù)關(guān)系式,并寫出x的取值范圍;
(2)求△PBQ的面積的最大值.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】二次函數(shù)y=ax2+bx+c(a≠0)的大致圖象如圖所示,頂點坐標為(﹣2,﹣9a),下列結(jié)論:①4a+2b+c>0;②5a﹣b+c=0;③若方程a(x+5)(x﹣1)=﹣1有兩個根x1和x2,且x1<x2,則﹣5<x1<x2<1;④若方程|ax2+bx+c|=1有四個根,則這四個根的和為﹣4.其中正確的結(jié)論有( )
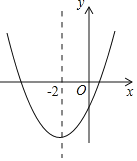
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】若二次函數(shù)y=ax2+bx+c的x與y的部分對應值如下表:則下列說法錯誤的是( )
x | … | -1 | 0 | 1 | 2 | 3 | … |
y | … |
|
|
|
|
| … |
A. 二次函數(shù)圖像與x軸交點有兩個
B. x≥2時y隨x的增大而增大
C. 二次函數(shù)圖像與x軸交點橫坐標一個在-1~0之間,另一個在2~3之間
D. 對稱軸為直線x=1.5
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,點![]() 、
、![]() 在函數(shù)
在函數(shù)![]() (
(![]() ,
,![]() 且
且![]() 是常數(shù))的圖像上,且點
是常數(shù))的圖像上,且點![]() 在點
在點![]() 的左側(cè)過點
的左側(cè)過點![]() 作
作![]() 軸,垂足為
軸,垂足為![]() ,過點
,過點![]() 作
作![]() 軸,垂足為
軸,垂足為![]() ,
,![]() 與
與![]() 的交點為
的交點為![]() ,連結(jié)
,連結(jié)![]() 、
、![]() .若
.若![]() 和
和![]() 的面積分別為1和4,則
的面積分別為1和4,則![]() 的值為( )
的值為( )

A.4B.![]() C.
C.![]() D.6
D.6
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
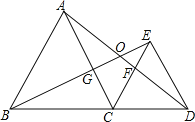
【題目】如圖,△ABC和△ECD都是等邊三角形,B、C、D三點在一條直線上,AD與BE相交于點O,AD與CE相交于點F,AC與BE相交于點G.
(1)△BCE與△ACD全等嗎?請說明理由.
(2)求∠BOD度數(shù).
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com