
【題目】(提出問題)課間,一位同學拿著方格本遇人便問:“如圖所示,在邊長為1的小正方形組成的網格中,點A、B、C都是格點,如何證明點A、B、C在同一直線上呢?”

(分析問題)一時間,大家議論開了. 同學甲說:“可以利用代數方法,建立平面直角坐標系,利用函數的知識解決”,同學乙說:“也可以利用幾何方法…”同學丙說:“我還有其他的幾何證法”……
(解決問題)請你用兩種方法解決問題
方法一(用代數方法):

方法二(用幾何方法):

【答案】(1)見詳解;(2)見詳解.
【解析】
(1)以點B為原點建立平面直角坐標系,則點C為(1,2),利用待定系數法求出直線BC的解析式,然后判斷點A是否在直線BC上即可;
(2)在格點中構造兩個三角形,證明△ABD≌△BCE,得到∠ABD=∠BCE,利用平角的定義,得到∠ABC=180°,即可得到點A、B、C在同一條直線上.
解:(1)如圖,以點B為原點建立平面直角坐標系,
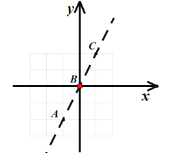
則點C坐標為(1,2),
設直線BC的解析式為:![]() ,
,
解得:![]() ,
,
∴直線BC的解析式為:![]() ;
;
當![]() 時,
時,![]() ,
,
∴點A(![]() )在直線BC上,
)在直線BC上,
∴A、B、C三點在同一條直線上;
(2)如圖,在網格中構造兩個三角形,△ABD和△BCE;
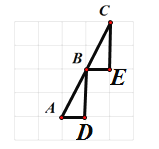
∵網格的邊長為1,
∴AD=BE=1,BD=CE=2,∠D=∠E=90°,
∴△ABD≌△BCE,
∴∠ABD=∠BCE,
∵∠BCE+∠CBE=90°,
∴∠ABD+∠CBE=90°,
∴∠ABC=∠ABD+∠DBE+∠CBE=90°+90°=180°,
∴A、B、C三點在同一條直線上.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】我們新定義一種三角形:若一個三角形中存在兩邊的平方差等于第三邊上高的平方,則稱這個三角形為勾股高三角形,兩邊交點為勾股頂點.
●特例感知
①等腰直角三角形 勾股高三角形(請填寫“是”或者“不是”);
②如圖1,已知△ABC為勾股高三角形,其中C為勾股頂點,CD是AB邊上的高.若![]() ,試求線段CD的長度.
,試求線段CD的長度.

●深入探究
如圖2,已知△ABC為勾股高三角形,其中C為勾股頂點且CA>CB,CD是AB邊上的高.試探究線段AD與CB的數量關系,并給予證明;

●推廣應用
如圖3,等腰△ABC為勾股高三角形,其中![]() ,CD為AB邊上的高,過點D向BC邊引平行線與AC邊交于點E.若
,CD為AB邊上的高,過點D向BC邊引平行線與AC邊交于點E.若![]() ,試求線段DE的長度.
,試求線段DE的長度.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點P在長方形OABC的邊OA上,連接BP,過點P作BP的垂線,交射線OC于點Q,在點P從點A出發沿AO方向運動到點O的過程中,設AP=x,OQ=y,則下列說法正確的是( )

A.y隨x的增大而增大B.y隨x的增大而減小
C.隨x的增大,y先增大后減小D.隨x的增大,y先減小后增大
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,AB=BC,將△ABC繞點B順時針旋轉α度,得到△A1BC1,A1B交AC于E,A1C1分別交AC、BC于點D、F,下列結論:①∠CDF=α,②A1E=CF,③DF=FC,④AD=CE,⑤A1F=CE.其中一定正確的有
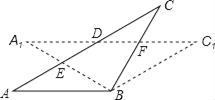
A. ①②④ B. ②③④ C. ①②⑤ D. ③④⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在Rt△ABC中,∠ACB=90°,AC=15,AB=25,點D為斜邊AB上動點.

(1)如圖1,當CD⊥AB時,求CD的長度;
(2)如圖2,當AD=AC時,過點D作DE⊥AB交BC于點E,求CE的長度;
(3)如圖3,在點D的運動過程中,連接CD,當△ACD為等腰三角形時,直接寫出AD的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,某地有一座圓弧形的拱橋,橋下水面寬AB為12米,拱高CD為4米.
(1)求這座拱橋所在圓的半徑.
(2)現有一艘寬5米,船艙頂部為正方形并高出水面3.6米的貨船要經過這里,此時貨船能順利通過這座拱橋嗎?請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖, BD 是△ABC 的角平分線, AE⊥ BD ,垂足為 F ,若∠ABC=35°,∠ C=50°,則∠CDE 的度數為( )
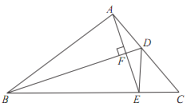
A.35°B.40°C.45°D.50°
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com