
【題目】如圖,連接四邊形ABCD各邊中點(diǎn),得到四邊形EFGH,還要添加 條件,才能保證四邊形EFGH是矩形.

【答案】AC⊥BD
【解析】菱形的判別方法是說(shuō)明一個(gè)四邊形為菱形的理論依據(jù),常用三種方法:①定義;②四邊相等;③對(duì)角線互相垂直平分.
解:添加AC=BD.
如圖,AC=BD,E、F、G、H分別是線段AB、BC、CD、AD的中點(diǎn),
則EH、FG分別是△ABD、△BCD的中位線,EF、HG分別是△ACD、△ABC的中位線
∴EH=FG=![]() BD,EF=HG=
BD,EF=HG=![]() AC,
AC,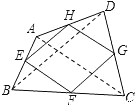
∴當(dāng)AC=BD時(shí),
EH=FG=FG=EF成立,
則四邊形EFGH是菱形.
“點(diǎn)睛”本題考查菱形的判定和三角形中位線定理.本題是開(kāi)放題,可以針對(duì)各種特殊的平行四邊形的判定方法,給出條件,再證明結(jié)論.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,這是一塊農(nóng)家菜地的平面圖,其中BD=4m,CD=3m,AB=13m,AC=12m,∠BDC=90°,則這塊地的面積為( )

A. 24m2 B. 30m2 C. 36m2 D. 42m2
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】八年級(jí)(1)班的體育委員把該年級(jí) 200 名同學(xué)的體育測(cè)試成績(jī)(得分均為整數(shù))進(jìn)行整理后分成5組,繪制出頻數(shù)分布直方圖(如圖).已知圖中從左到右的第一、第二、第三、第五小組的頻率分別是 0.05,0.10,0.30,0.15.回答下列問(wèn)題:
(1) 第四小組的頻率是多少?頻數(shù)是多少?
(2) 該年級(jí)規(guī)定測(cè)試成績(jī)?cè)?80 分以上的為A ![]() 級(jí),60 分以下的為C 級(jí),其余為B 級(jí).為了反映測(cè)試成績(jī)不同等級(jí)的人數(shù)所占總體的百分比情況,你認(rèn)為用哪種統(tǒng)計(jì)圖比較合理?
級(jí),60 分以下的為C 級(jí),其余為B 級(jí).為了反映測(cè)試成績(jī)不同等級(jí)的人數(shù)所占總體的百分比情況,你認(rèn)為用哪種統(tǒng)計(jì)圖比較合理?
(3) 如果有一位體育測(cè)試成績(jī)?yōu)?5 分的同學(xué)轉(zhuǎn)學(xué)來(lái)到該年級(jí),那么在重新統(tǒng)計(jì)后,與原來(lái)的頻率相比,哪些等級(jí)的頻率發(fā)生了改變?變大了還是變小了?

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某人的身份證號(hào)碼為320621198602187913,則此人出生于______年_______月_______日.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,四邊形ABCD中,對(duì)角線AC、BD相交于點(diǎn)O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.
(1)求證:四邊形ABCD是矩形.
(2)若∠ADF:∠FDC=3:2,DF⊥AC,則∠BDF的度數(shù)是多少?

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】將拋物線y=3x2+2向左平移2個(gè)單位長(zhǎng)度,再向下平移3個(gè)單位長(zhǎng)度,則得到的拋物線的解析式為( )
A. y=3(x﹣2)2﹣1 B. y=3(x﹣2)2+5
C. y=3(x+2)2﹣1 D. y=3(x+2)2+5
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知一個(gè)三角形的兩邊長(zhǎng)分別為3和4,則第三邊的長(zhǎng)不可能的是( )
A.2
B.3
C.4
D.1
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com