
【題目】在數學學習中,及時對知識進行歸納和整理是改善學習的重要方法善于學習的小明在學習了一次方程(組)、一元一次不等式和一次函數后,對相關知識進行了歸納整理.
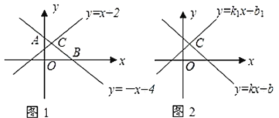
(1)例如他在同一個平面直角坐標系中畫出了一次函數![]() 和
和![]() 的圖像如圖(a)所示,并做了歸納:
的圖像如圖(a)所示,并做了歸納:
(Ⅰ)一次函數與方程的關系:
(ⅰ)一次函數的解析式就是一個二元一次方程.
(ⅱ)點B的橫坐標是方程①的解.
(ⅲ)點C的坐標![]() 中的x,y的值是方程組②的解.
中的x,y的值是方程組②的解.
(Ⅱ)一次函數與不等式的關系:
(ⅰ)函數![]() 的函數值y大于0時,自變量x的取值范圍就是不等式③的解集.
的函數值y大于0時,自變量x的取值范圍就是不等式③的解集.
(ⅱ)函數![]() 的函數值小于0時,自變量x的取值范圍就是不等式④的解集.
的函數值小于0時,自變量x的取值范圍就是不等式④的解集.
請根據圖(1)和以上方框中的內容,在下面數字序號后寫出相應的結論:①________;②________;③________;④________;
(2)若已知一次函數![]() 和
和![]() 的圖像,如圖(2)所示,且它們的交點C的坐標為
的圖像,如圖(2)所示,且它們的交點C的坐標為![]() ,那么不等式
,那么不等式![]() 的解集是________.
的解集是________.
【答案】(1)①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ;(2)
;(2)![]()
【解析】
(1)①點B是直線![]() 與x軸的交點,即y=0,即可得出方程;②將兩條直線解析式聯立方程組即可;③y>0,即
與x軸的交點,即y=0,即可得出方程;②將兩條直線解析式聯立方程組即可;③y>0,即![]() ;④函數
;④函數![]() 的函數值小于0,即
的函數值小于0,即![]() ;
;
(2)觀察圖象,當直線![]() 在直線
在直線![]() 上方時(含交點),對應的x取值范圍即為不等式的解集.
上方時(含交點),對應的x取值范圍即為不等式的解集.
(1)①∵點B是直線![]() 與x軸的交點,即y=0
與x軸的交點,即y=0
∴點B的橫坐標是方程![]() 的解
的解
②點C的坐標![]() 中的x,y的值是方程組
中的x,y的值是方程組![]() 的解
的解
③函數![]() 的函數值y大于0時,即
的函數值y大于0時,即![]()
∴自變量x的取值范圍就是不等式![]() 的解集
的解集
④函數![]() 的函數值小于0,即
的函數值小于0,即![]() ,
,
∴自變量x的取值范圍就是不等式![]() 的解集
的解集
故答案為:![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(2)觀察圖象,當直線![]() 在直線
在直線![]() 上方時(含交點),
上方時(含交點),
對應的x取值范圍是![]()
∴不等式![]() 的解集是
的解集是![]() .
.


 一課一練課時達標系列答案
一課一練課時達標系列答案科目:初中數學 來源: 題型:
【題目】已知:如圖![]() ,
,![]() 是
是![]() 的平分線,點
的平分線,點![]() 在
在![]() 上,
上,![]() ,且點
,且點![]() 到
到![]() 的距離為
的距離為![]() ,過點
,過點![]() 作
作![]() ,
,![]() ,垂足分別為
,垂足分別為![]() ,
,![]() ,易得到結論:
,易得到結論:![]() .
.
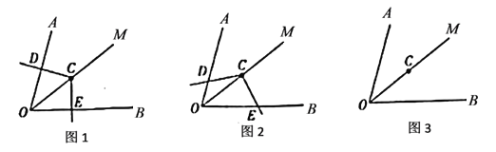
(1)把圖![]() 中的
中的![]() 繞點
繞點![]() 旋轉,當
旋轉,當![]() 與
與![]() 不垂直時(如圖
不垂直時(如圖![]() ),上述結論是否成立?并說明理由.
),上述結論是否成立?并說明理由.
(2)把圖![]() 中的
中的![]() 繞點
繞點![]() 旋轉,當
旋轉,當![]() 與
與![]() 的反向延長線相交于點
的反向延長線相交于點![]() 時:
時:
①請在圖![]() 中畫出圖形;
中畫出圖形;
②上述結論還成立嗎?若成立,請給出證明;若不成立,請直接寫出線段![]() ,
,![]() 之間的的數量關系,不需證明.
之間的的數量關系,不需證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖形變換中的數學,問題情境:在課堂上,興趣學習小組對一道數學問題進行了深入探究,在Rt△ABC中,∠ACB=90°,∠A=30°,點D是AB的中點,連接CD.探索發現:
(1)如圖①,BC與BD的數量關系是 ;
(2)如圖①,CD與AB的數量關系是 ;并說明理由.
猜想驗證:
(3)如圖②,若P是線段CB上一動點(點P不與點B,C重合),連接DP,將線段DP繞點D逆時針旋轉60°,得到線段DF,連接BF,請猜想BF,BP,BD三者之間的數量關系,并證明你的結論;
拓展延伸:
(4)若點P是線段CB延長線上一動點,按照(3)中的作法,請在圖③中補全圖象,并直接寫出BF、BP、BD三者之間的數量關系.

查看答案和解析>>
科目:初中數學 來源: 題型:
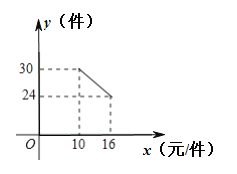
【題目】一名在校大學生利用“互聯網+”自主創業,銷售一種產品,這種產品成本價10元/件,已知銷售價不低于成本價,且物價部門規定這種產品的銷售價不高于16元/件,市場調查發現,該產品每天的銷售量y(件)與銷售價x(元/件)之間的函數關系如圖所示.
(1)求y與x之間的函數關系式,并寫出自變量x的取值范圍;
(2)求每天的銷售利潤W(元)與銷售價x(元/件)之間的函數關系式,并求出每件銷售價為多少元時,每天的銷售利潤最大?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)讀讀做做:教材中有這樣的問題,觀察下面的式子,探索它們的規律,![]() =1-
=1-![]() ,
,![]() =
=![]() ,
,![]() =
=![]() ……用正整數n表示這個規律是______;
……用正整數n表示這個規律是______;
(2)問題解決:一容器裝有1L水,按照如下要求把水倒出:第一次倒出![]() L水,第二次倒出的水量是
L水,第二次倒出的水量是![]() L水的
L水的![]() ,第三次倒出的水量是
,第三次倒出的水量是![]() L水的
L水的![]() ,第四次倒出的水量是
,第四次倒出的水量是![]() L水的
L水的![]() ,……,第n+1次倒出的水量是
,……,第n+1次倒出的水量是![]() L水的
L水的![]() ,……,按照這種倒水方式,這1L水能否倒完?
,……,按照這種倒水方式,這1L水能否倒完?
(3)拓展探究:①解方程:![]() +
+![]() +
+![]() +
+![]() =
=![]() ;
;
②化簡:![]() +
+![]() +
+![]() …+
…+![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 中,
中,![]() ,
,![]() ,點
,點![]() 為直線
為直線![]() 上一動點(點
上一動點(點![]() 不與
不與![]() 、
、![]() 重合),以
重合),以![]() 為邊在
為邊在![]() 右側作等腰直角三角形
右側作等腰直角三角形![]() ,使
,使![]() ,連接
,連接![]() .
.
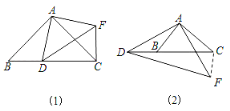
(1)如圖1,當點![]() 在線段
在線段![]() 上時;證明
上時;證明
①![]()
②![]()
(2)如圖2,當點![]() 在線段
在線段![]() 的延長線上時,結論(1)中的①、②是否仍然成立?若成立,請給予證明:若不成立,請你寫出正確結論再給予證明.
的延長線上時,結論(1)中的①、②是否仍然成立?若成立,請給予證明:若不成立,請你寫出正確結論再給予證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
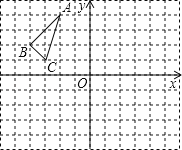
【題目】△ABC在平面直角坐標系中的位置如圖,其中每個小正方形的邊長為1個單位長度.
(1)按要求作圖:
①畫出△ABC關于原點O的中心對稱圖形△A1B1C1;
②畫出將△ABC繞點C順時針旋轉90°得到△A2B2C2.
(2)回答下列問題:
①△A1B1C1中頂點A1坐標為 ;
②若P(a,b)為△ABC邊上一點,則按照(1)中①作圖,點P對應的點P1的坐標為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
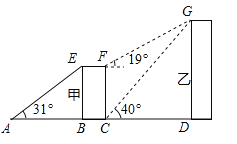
【題目】某學校教學樓(甲樓)的頂部E和大門A之間掛了一些彩旗.小穎測得大門A距甲樓的距離AB是31cm,在A處測得甲樓頂部E處的仰角是31°.
(1)求甲樓的高度及彩旗的長度;(精確到0.01m)
(2)若小穎在甲樓樓底C處測得學校后面醫院樓(乙樓)樓頂G處的仰角為40°,爬到甲樓樓頂F處測得乙樓樓頂G處的仰角為19°,求乙樓的高度及甲乙兩樓之間的距離.(精確到0.01m)
(cos31°≈0.86,tan31°≈0.60,cos19°≈0.95,tan19°≈0.34,cos40°≈0.77,tan40°≈0.84)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com