
【題目】如圖,已知直線![]() ,
,![]() 分別是直線
分別是直線![]() 上的點.
上的點.
(1)在圖1中,判斷![]() 和
和![]() 之間的數量關系,并證明你的結論;
之間的數量關系,并證明你的結論;
(2)在圖2中,請你直接寫出![]() 和
和![]() 之間的數量關系(不需要證明);
之間的數量關系(不需要證明);
(3)在圖3中,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,且
,且![]() ,求
,求![]() 的度數.
的度數.

【答案】(1)![]() ,證明見析;(2)
,證明見析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)如圖,過點![]() 作直線
作直線![]() ,由平行線的性質得到
,由平行線的性質得到![]() ,
,![]() ,即可求得
,即可求得![]() ;
;
(2)如圖,記AB與NE的交點為G,由平行線的性質得∠EGM=∠DNE,由三角形外角性質得∠BME=∠MEN+∠EGM,由此即可得到結論;
(3)由角平分線的定義設![]() ,設
,設![]() ,由(1),得
,由(1),得![]() ,由(2),得
,由(2),得![]() ,再根據
,再根據![]() ,可求得
,可求得![]() ,繼而可求得
,繼而可求得![]() .
.
(1)![]() ,證明如下:
,證明如下:
如圖,過點![]() 作直線
作直線![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;

(2)![]() ,理由如下:
,理由如下:
如圖,記AB與NE的交點為G,
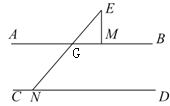
又∵AB//CD,
∴∠EGM=∠DNE,
∵∠BME是△EMG的外角,
∴∠BME=∠MEN+∠EGM,
∴∠MEN=∠BME-∠DNE;
(3)∵![]() 平分
平分![]() ,
,
∴設![]() ,
,
∵![]() 平分
平分![]() ,
,
∴設![]() ,
,
由(1),得![]() ,
,
由(2),得![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() .
.


 金鑰匙試卷系列答案
金鑰匙試卷系列答案科目:初中數學 來源: 題型:
【題目】一副三角板如圖擺放,點F是 45°角三角板△ABC的斜邊的中點,AC=4.當 30°角三角板DEF的直角頂點繞著點F旋轉時,直角邊DF,EF分別與AC,BC相交于點 M, N.在旋轉過程中有以下結論:①MF=NF;②CF與MN可能相等嗎;③MN 長度的最小值為 2;④四邊形CMFN的面積保持不變; ⑤△CMN面積的最大值為 2.其中正確的個數是_________.(填寫序號).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為提高飲水質量,越來越多的居民選購家用凈水器.我市飛龍商場抓住商機,從廠家購進了A、B兩種型號家用凈水器共100臺,A型號家用凈水器進價是150元/臺,B型號家用凈水器進價是250元/臺,購進兩種型號的家用凈水器共用去19000 元.
(1)求A、B兩種型號家用凈水器各購進了多少臺;
(2)為使每臺B型號家用凈水器的毛利潤是A型號的2倍,且保證售完這100臺家用凈水器的毛利潤不低于5600元,求每臺A型號家用凈水器的售價至少是多少元? (注: 毛利潤=售價一進價) .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知:∠MON=30°,點A1、A2、A3 在射線ON上,點B1、B2、B3…在射線OM上,△A1B1A2、△A2B2A3、△A3B3A4…均為等邊三角形,若OA1=a,則△A6B6A7的邊長為______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】通過類比聯想、引申拓展研究典型題目,可達到解一題知一類的目的.下面是一個案例,請補充完整.

原題:如圖1,點E、F分別在正方形ABCD的邊BC、CD上,∠EAF=45°,連接EF,則EF=BE+DF,試說明理由.
(1)思路梳理
∵AB=CD,
∴把△ABE繞點A逆時針旋轉90°至△ADG,可使AB與AD重合.
∵∠ADC=∠B=90°,
∴∠FDG=180°,點F、D、G共線.
根據___________,SAS
易證△AFG≌___________△AEF
,得EF=BE+DF.
(2)類比引申
如圖2,四邊形ABCD中,AB=AD,∠BAD=90°.點E、F分別在邊BC、CD上,∠EAF=45°.若∠B、∠D都不是直角,則當∠B與∠D滿足等量關系______________∠B+∠D=180°
時,仍有EF=BE+DF.
(3)聯想拓展
如圖3,在△ABC中,∠BAC=90°,AB=AC,點D、E均在邊BC上,且∠DAE=45°.猜想BD、DE、EC應滿足的等量關系,并寫出推理過程.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們把1°的圓心角所對的弧叫做1°的弧,則圓心角AOB的度數等于它所對的弧AB的度數記為:∠AOB![]()
![]() .由此可知:命題“圓周角的度數等于其所對的弧的度數的一半.”是真命題,請結合圖形1給予證明(不要求寫已知、求證,只需直接證明),并解決以下的問題(1)和問題(2).
.由此可知:命題“圓周角的度數等于其所對的弧的度數的一半.”是真命題,請結合圖形1給予證明(不要求寫已知、求證,只需直接證明),并解決以下的問題(1)和問題(2).
問題(1):如圖2,⊙O的兩條弦AB、CD相交于圓內一點P,求證:∠APC![]()
![]() (
(![]() +
+![]() );
);
問題(2):如圖3,⊙O的兩條弦AB、CD相交于圓外一點P,問題(1)中的結論是否成立,如果成立,給予證明;如果不成立,寫出一個類似的結論(不要求證明)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知正方形![]() (四邊相等,四個角都是直角),點
(四邊相等,四個角都是直角),點![]() 為邊
為邊![]() 上異于點
上異于點![]() 的一動點,
的一動點,![]() ,交
,交![]() 于點
于點![]() ,點
,點![]() 為
為![]() 延長線上一定點,滿足
延長線上一定點,滿足![]() ,
,![]() 的延長線與
的延長線與![]() 交于點
交于點![]() ,連接
,連接![]() .
.
(1)判斷![]() 是 三角形.
是 三角形.
(2)求證: ![]() ≌
≌![]() .
.
(3)探究![]() 是否為定值?如果是定值,請說明理由,并求出該定值;如果不是定值,請說明理由.
是否為定值?如果是定值,請說明理由,并求出該定值;如果不是定值,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
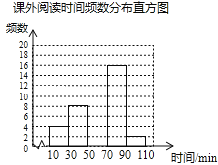
【題目】某學校為了解學生的課外閱讀情況,隨機抽取了50名學生,并統計他們平均每天的課外閱讀時間t(單位:min),然后利用所得數據繪制成如下不完整的統計表.
課外閱讀時間t | 頻數 | 百分比 |
10≤t<30 | 4 | 8% |
30≤t<50 | 8 | 16% |
50≤t<70 | a | 40% |
70≤t<90 | 16 | b |
90≤t<110 | 2 | 4% |
合計 | 50 | 100% |
請根據圖表中提供的信息回答下列問題:
(1)a= ,b= ;
(2)將頻數分布直方圖補充完整;
(3)若全校有900名學生,估計該校有多少學生平均每天的課外閱讀時間不少于50min?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位線,點M是邊BC上一點,BM=3,點N是線段MC上的一個動點,連接DN,ME,DN與ME相交于點O.若△OMN是直角三角形,則DO的長是______.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com