
【題目】在平面直角坐標系中,已知如圖所示的拋物線頂點![]() 的坐標為
的坐標為![]() ,且過點
,且過點![]() .
.
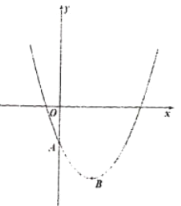
(1)求該拋物線的解析式;
(2)若點![]() 為拋物線對稱軸右側、
為拋物線對稱軸右側、![]() 軸下方一點,當
軸下方一點,當![]() 時,求直線
時,求直線![]() 的解析式;
的解析式;
(3)平移(1)中的拋物線,記平移后拋物線的頂點為![]() ,頂點
,頂點![]() 在直線
在直線![]() 上滑動,且平移后的拋物線與直線
上滑動,且平移后的拋物線與直線![]() 交于另一點
交于另一點![]() ,若點
,若點![]() 為平移前(1)中拋物線上的點,則當以
為平移前(1)中拋物線上的點,則當以![]() 、
、![]() 、
、![]() 三點為頂點的三角形是等腰直角三角形時,求出所有符合條件的點
三點為頂點的三角形是等腰直角三角形時,求出所有符合條件的點![]() 的坐標.
的坐標.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)符合條件的點E的坐標為(4,-2)或(-2,4)或(
;(3)符合條件的點E的坐標為(4,-2)或(-2,4)或(![]() )或(
)或(![]() ).
).
【解析】
(1)由頂點坐標,設拋物線![]() ,然后將A點代入解析式,用待定系數法求解即可;
,然后將A點代入解析式,用待定系數法求解即可;
(2)過點B作BN⊥y軸,直線OP與拋物線對稱抽BM交于點F,結合矩形的性質求得![]() ,從而得到FO=FB,設MF=x,則FO=FB=4-x,利用勾股定理求x的值,確定F點坐標,從而用待定系數法求直線解析式;
,從而得到FO=FB,設MF=x,則FO=FB=4-x,利用勾股定理求x的值,確定F點坐標,從而用待定系數法求直線解析式;
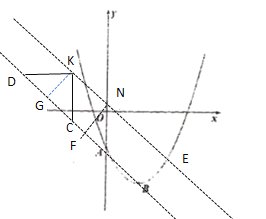
(3)線段AB的長度可求,并且在拋物線滑動過程中,線段CD的長度也是不變的,始終等于AB,因此,問題就相當于一條定長線段CD在直線AB上滑動,若![]() 、
、![]() 、
、![]() 三點為頂點的三角形是等腰直角三角形,則按照∠KDC=90°,KD=DC;∠KCD=90°,KC=DC;∠CKD=90°,CK=DK三種情況分析,只需利用等腰直角三角形和一次函數的圖像性質求得AN的相應的距離,從而求平移后的直線解析式與原拋物線解析式相等時方程的解,可解得E點的坐標.
三點為頂點的三角形是等腰直角三角形,則按照∠KDC=90°,KD=DC;∠KCD=90°,KC=DC;∠CKD=90°,CK=DK三種情況分析,只需利用等腰直角三角形和一次函數的圖像性質求得AN的相應的距離,從而求平移后的直線解析式與原拋物線解析式相等時方程的解,可解得E點的坐標.
解:(1)由題意,設拋物線![]() ,將
,將![]() 代入,得
代入,得
![]() ,解得:
,解得:![]()
∴拋物線的解析式為:![]()
(2)如圖:過點B作BN⊥y軸,直線OP與拋物線對稱抽BM交于點F
由題意可知![]() ,四邊形ONBM是矩形
,四邊形ONBM是矩形
∴![]()
∴![]()
∴FO=FB
由B(2,-4)可得,OM=2,MB=4
設MF=x,則FO=FB=4-x
在Rt△OMF中,![]() ,解得:
,解得:![]()
∴F(2,![]() )
)
設直線OP的解析式為![]() ,把F(2,
,把F(2,![]() )代入,得
)代入,得![]()
解得:![]()
∴直線OP的解析式為![]() ;
;
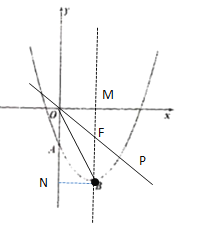
(3)∵A(0,-2),B(2,-4)
∴![]()
拋物線滑動過程中,C與B為對應點,D與A為對應點,
∴![]()
∴①當∠KDC=90°,KD=DC=![]() 時,
時,
設過點K且平行于直線AB的直線KN(直線KN與y軸交于點N)的解析式為y=-x+n
設直線AB的解析式為![]() ,則
,則![]() 解得
解得![]()
所以直線AB的解析式為:y=-x-2
∴∠FAN=45°,
∴△NFA為等腰直角三角形,則![]()
∴N(0,2)
則直線KN的解析式為y=-x+2
由此![]() ,解得
,解得![]() 或
或![]()
∴E點坐標為(4,-2)或(-2,4)
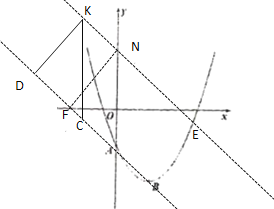
②當∠KCD=90°,KC=DC=![]() 時,同理可求,E點坐標為(4,-2)或(-2,4);
時,同理可求,E點坐標為(4,-2)或(-2,4);
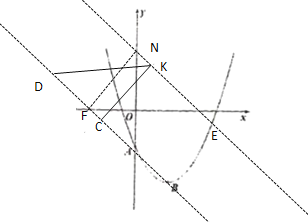
③當∠CKD=90°,CK=DK時,
過點K作KG⊥CD,此時,KG=NF=AF=![]() ,AN=2
,AN=2
∴N(0,0)
則直線KN的解析式為y=-x
由此![]() ,解得
,解得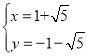 或
或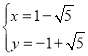
∴E點坐標為(![]() )或(
)或(![]() )
)
綜上所述,符合條件的點E的坐標為(4,-2)或(-2,4)或(![]() )或(
)或(![]() ).
).


科目:初中數學 來源: 題型:
【題目】如圖①,在△ABC中,AB=AC,∠BAC=![]() (
(![]() <45°).先將△ABC以點B為旋轉 中心,逆時針旋轉90°得到△DBE,再將△ABC以點A為旋轉中心,順時針旋轉90°得到△AFG,連接DF,DG,AE,如圖②.
<45°).先將△ABC以點B為旋轉 中心,逆時針旋轉90°得到△DBE,再將△ABC以點A為旋轉中心,順時針旋轉90°得到△AFG,連接DF,DG,AE,如圖②.
(1)四邊形ABDF的形狀是 ;
(2)求證:四邊形AEDG是平行四邊形;
(3)若AB=2,![]() =30°,則四邊形AEDG的面積是 .
=30°,則四邊形AEDG的面積是 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對垃圾進行分類投放,能提高垃圾處理和再利用的效率,減少污染,保護環境.為了檢查垃圾分類的落實情況,某居委會成立了甲、乙兩個檢查組,采取隨機抽查的方式分別對轄區內的A,B,C,D四個小區進行檢查,并且每個小區不重復檢查.
(1)甲組抽到A小區的概率是多少;
(2)請用列表或畫樹狀圖的方法求甲組抽到A小區,同時乙組抽到C小區的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知如圖,拋物線![]() 與
與![]() 軸交于點A和點C(2,0),與
軸交于點A和點C(2,0),與![]() 軸交于點D,將△DOC繞點O逆時針旋轉90°后,點D恰好與點A重合,點C與點B重合.
軸交于點D,將△DOC繞點O逆時針旋轉90°后,點D恰好與點A重合,點C與點B重合.
(1)直接寫出點A和點B的坐標;
(2)求![]() 和
和![]() 的值;
的值;
(3)已知點E是該拋物線的頂點,求證:AB⊥EB.

查看答案和解析>>
科目:初中數學 來源: 題型:
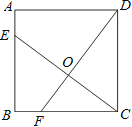
【題目】如圖,已知正方形ABCD的邊長為4,點E、F分別在邊AB、BC上,且AE=BF=1,CE、DF交于點O.下列結論:①∠DOC=90°, ②OC=OE, ③tan∠OCD =![]() ,④
,④![]() 中,正確的有( )
中,正確的有( )
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
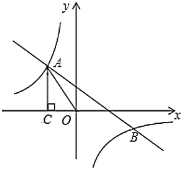
【題目】如圖,一次函數![]() 的圖象與反比例函數
的圖象與反比例函數![]() 的圖象交于第二、四象限內的點
的圖象交于第二、四象限內的點![]() 和點
和點![]() .過點
.過點![]() 作
作![]() 軸的垂線,垂足為點
軸的垂線,垂足為點![]() ,
,![]() 的面積為4.若在
的面積為4.若在![]() 軸上取點
軸上取點![]() ,則當
,則當![]() 取得最大值時,點
取得最大值時,點![]() 的坐標為______.
的坐標為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,以ABCD 的四條邊為邊,分別向外作正方形,連結 EF,GH,IJ,KL.如果ABCD 的 面積為 8,則圖中陰影部分四個三角形的面積和為( )

A.8B.12C.16D.20
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com