
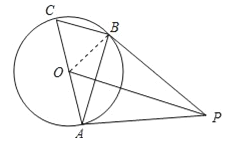
【題目】如圖,AC是⊙O的直徑,BC是⊙O的弦,點P是⊙O外一點,連接PA,PB,AB,已知∠PBA=∠C.

(1)求證:PB是⊙O的切線;
(2)連接OP,若OP∥BC,且OP=8,⊙O的半徑為![]() ,求BC的長.
,求BC的長.
【答案】(1)詳見解析;(2)BC=2.
【解析】試題分析:(1)連接OB,由圓周角定理得出∠ABC=90°,得出∠C+∠BAC=90°,再由OA=OB,得出∠BAC=∠OBA,證出∠PBA+∠OBA=90°,即可得出結論;
(2)證明△ABC∽△PBO,得出對應邊成比例,即可求出BC的長.
試題解析:(1)證明:連接OB,如圖所示:
∵AC是⊙O的直徑,
∴∠ABC=90°,
∴∠C+∠BAC=90°,
∵OA=OB,
∴∠BAC=∠OBA,
∵∠PBA=∠C,
∴∠PBA+∠OBA=90°,
即PB⊥OB,
∴PB是⊙O的切線;
(2)解:∵⊙O的半徑為2![]() ,
,
∴OB=2![]() ,AC=4
,AC=4![]() ,
,
∵OP∥BC,
∴∠C=∠BOP,
又∵∠ABC=∠PBO=90°,
∴△ABC∽△PBO,
∴![]() ,
,
即![]() ,
,
∴BC=2.


科目:初中數學 來源: 題型:
【題目】(在矩形ABCD中,AB=4,BC=8,經過對角線交點O的直線EF繞點O旋轉,分別交AD、BC于點E、F,連接AF、CE.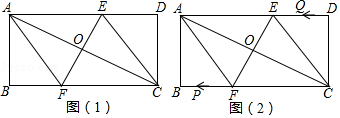
(1)如圖(1),依據下列條件在普通四邊形、梯形、普通平行四邊形、矩菱形或正方形中選擇填空:旋轉過程中四邊形AFCE始終為;
當點E為AD的中點時四邊形AFCE為;
當EF⊥AC時四邊形AFCE為;
(2)如圖(1),當EF⊥AC時,求AF的長;
(3)如圖(2),在(2)的基礎上,若動點P從A點出發,沿A→F→B→A運動一周停止,速度為每秒5厘米;同時點Q從C點出發,沿C→D→E→C運動一周停止,速度為每秒4厘米,在P、Q運動過程中,第幾秒時,四邊形APCQ是平行四邊形?
查看答案和解析>>
科目:初中數學 來源: 題型:
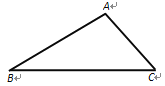
【題目】如圖,在△ABC中,
(1)在圖中作出△ABC的內角平分線AD.(要求:尺規作圖,保留作圖痕跡,不寫證明過程)
(2)若∠BAC = 2∠C,在已作出的圖形中,△ ∽△
(3)畫出△ABC的高AE(使用三角板畫出即可),若∠B=α,∠C=β,那么∠DAE= (請用含α、β的代數式表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲,乙,丙三家超市為了促銷一種定價均為m元的商品,甲超市連續兩次降價20%,乙超市一次性降價40%,丙超市第一次降價30%,第二次降價10%,此時顧客要購買這種商品最劃算應到的超市是( )
A.甲
B.乙
C.丙
D.乙或丙
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com