
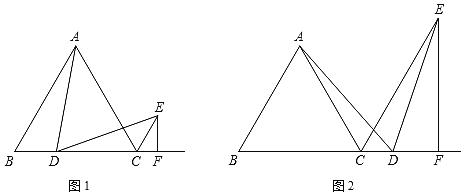
【題目】在等邊△ABC中,D為射線BC上一點,CE是∠ACB外角的平分線,∠ADE=60°,EF⊥BC于F.
(1)如圖1,若點D在線段BC上,證明:∠BAD=∠EDC;
(2)如圖1,若點D在線段BC上,證明:①AD=DE;②BC=DC+2CF(提示:構造全等三角形);
(3)如圖2,若點D在線段BC的延長線上,直接寫出BC、DC、CF三條線段之間的數量關系.
【答案】(1)見解析;(2)①見解析;②見解析;(3)BC=2CF-DC;理由見解析.
【解析】
(1)由等邊三角形的性質得出∠B=60°,再由三角形的外角性質結合已知條件,即可得出結論;
(2)過D作DG∥AC交AB延長線于G,證得△AGD≌△DCE,得出:①AD=DE;進一步利用GD=CE,BD=CE得出②BC=DC+2CF;
(3)過D作DG∥AC交AB延長線于G,由平行線和等邊三角形的性質得出∠BGD=∠BDG=∠B=60°,證出△GBD是等邊三角形,證出AG=CD,再證出∠GAD=∠CDE,證明△AGD≌△DCE,得出GD=CE,進而得出結論.
(1)∵△ABC是等邊三角形,
∴∠B=60°,
∵∠ADC=∠ADE+∠EDC=∠B+∠BAD,∠ADE=60°,
∴∠BAD=∠EDC;
(2)①過D作DG∥AC交AB于G,如圖1所示:

∵△ABC是等邊三角形,AB=BC,
∴∠B=∠ACB=60°,
∴∠BDG=∠ACB=60°,
∴∠BGD=60°,
∴△BDG是等邊三角形,
∴BG=BD,∠AGD=∠B+∠BDG=60°+60°=120°,
∴AG=DC,
∵CE是∠ACB外角的平分線,
∴∠DCE=120°=∠AGD,
由(1)知∠GAD=∠EDC,
在△AGD和△DCE中,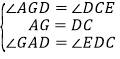 ,
,
∴△AGD≌△DCE(ASA),
∴AD=DE;
②∵△AGD≌△DCE,
∴GD=CE,
∴BD=CE,
∵EF⊥BC,CE是∠ACB外角的平分線,
∴∠ECF=60°,∠CEF=30°,
∴CE=2CF,
∴BC=CE+DC=DC+2CF;
(3)BC=2CF-DC;理由如下:
過D作DG∥AC交AB延長線于G,如圖2所示:
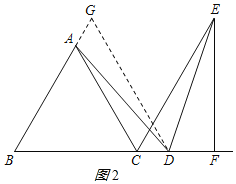
∵DG∥AC,△ABC是等邊三角形,
∴∠BGD=∠BDG=∠B=60°,
∴△GBD是等邊三角形,
∴GB-AB=DB-BC,即AG=DC,
∵∠ACB=60,CE是∠ACB的外角平分線,
∴∠DCE=∠ACE=![]() ×(180°-∠ACB)=60°,
×(180°-∠ACB)=60°,
∴∠AGD=∠DCE=60°,
∵∠GAD=∠B+∠ADC=60°+∠ADC,
∠CDE=∠ADC+∠ADE=∠ADC+60°,
∴∠GAD=∠CDE,
在△AGD和△DCE中,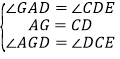 ,
,
∴△AGD≌△DCE(ASA),
∴GD=CE,
∴BD=CE,
∵CE=2CF,
∴BC=BD-DC=CE-DC=2CF-DC.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】一張桌子可坐6人,按下列方式將桌子拼在一起.

①2張桌子拼在一起可坐_____人,4張桌子拼在一起可坐_______人,![]() 張桌子拼在一起可坐(_____________)人.
張桌子拼在一起可坐(_____________)人.
②一家餐廳有40張這樣的長方形桌子,按照上圖方式每5張拼成一張大桌子,則40張桌子可拼成8張大桌子,共可坐__________人.
③若在②中,改成8張桌子拼成一張大桌子,則共可坐________人.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:在△ABC中,且∠BAC=70°,AD是△ABC的角平分線,點E是AC邊上的一點,點F為直線AB上的一動點,連結EF,直線EF與直線AD交于點P,設∠AEF=α°
(1)如圖①,若 DE//AB,則①∠ADE的度數是_______;
②當∠DPE=∠DEP時,∠AEF= _____度:當∠PDE=∠PED,∠AEF=_______度;
(2)如圖②,若DE⊥AC,則是否存在這樣的α的值,使得△DPE中有兩個相等的角?若存在求出α的值;若不存在,說明理由

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數y=ax2+bx+c(a≠0)的圖像與x軸交于A、B兩點,與y軸交于C點,且對稱軸為直線x=1,點B坐標為(-1,0).則下面的四個結論:①2a+b=0;②4a-2b+c<0;③ac>0;④當y<0時,x<-1或x>3.其中正確的個數是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
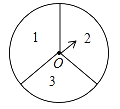
【題目】如圖,有一個可以自由轉動的轉盤被平均分成3個扇形,分別標有1,2,3三個數字.小王和小李各轉動一次轉盤為一次游戲,當每次轉盤停止后,指針所指扇形內的數為各自所得的數,一次游戲結束后得到一組數(若指針指在分界線時重轉).
(1)請你用樹狀圖或列表的方法表示出每次游戲可能出現的所有結果;
(2)求每次游戲后得到的一組數恰好是方程x2﹣4x+3=0的解的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
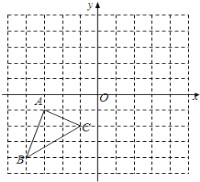
【題目】如圖,正方形網格中,每個小方格都是邊長為1的正方形,△ABC的三個頂點都在格點上,結合所給的平面直角坐標系解答下列問題:
(1)△ABC的面積為 ;
(2)將△ABC繞原點O 旋轉180°,畫出旋轉后的△A1B1C1;
(3)將△ABC向右平移4個單位長度,畫出平移后的△A2B2C2;
(4)△A1B1C1與△A2B2C2成中心對稱嗎?若是,請直接寫出對稱中心的坐標: .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】每到春夏交替時節,雌性楊樹會以滿天飛絮的方式來傳播下一代,漫天飛舞的楊絮易引發皮膚病、呼吸道疾病等,給人們造成困擾,為了解市民對治理楊絮方法的贊同情況,某課題小組隨機調查了部分市民(問卷調查表如表所示),并根據調查結果繪制了如下尚不完整的統計圖.
治理楊絮一一您選哪一項?(單選)
A.減少楊樹新增面積,控制楊樹每年的栽種量
B.調整樹種結構,逐漸更換現有楊樹
C.選育無絮楊品種,并推廣種植
D.對雌性楊樹注射生物干擾素,避免產生飛絮
E.其他
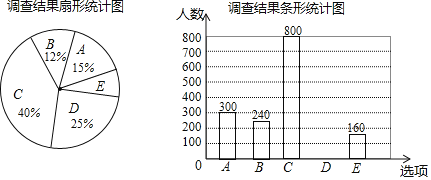
根據以上統計圖,解答下列問題:
(1)本次接受調查的市民共有 人;
(2)扇形統計圖中,扇形E的圓心角度數是 ;
(3)請補全條形統計圖;
(4)若該市約有90萬人,請估計贊同“選育無絮楊品種,并推廣種植”的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在△ABC中,AD是BC邊上的高,∠C=30°,∠ABC=45°,BE是AC邊上的中線.
(1)求證:AC=2BD;
(2)求∠CBE的度數;
(3)若點E到邊BC的距離為![]() ,求BC的長.
,求BC的長.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com