
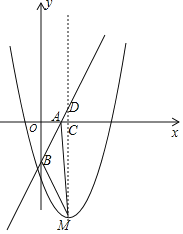
【題目】已知二次函數(shù)y=ax2﹣2ax﹣2的圖象(記為拋物線C1)頂點為M,直線l:y=2x﹣a與x軸,y軸分別交于A,B.
(1)對于拋物線C1,以下結(jié)論正確的是 ;
①對稱軸是:直線x=1;②頂點坐標(1,﹣a﹣2);③拋物線一定經(jīng)過兩個定點.
(2)當a>0時,設△ABM的面積為S,求S與a的函數(shù)關(guān)系;
(3)將二次函數(shù)y=ax2﹣2ax﹣2的圖象C1繞點P(t,﹣2)旋轉(zhuǎn)180°得到二次函數(shù)的圖象(記為拋物線C2),頂點為N.
①當﹣2≤x≤1時,旋轉(zhuǎn)前后的兩個二次函數(shù)y的值都會隨x的增大而減小,求t的取值范圍;
②當a=1時,點Q是拋物線C1上的一點,點Q在拋物線C2上的對應點為Q',試探究四邊形QMQ'N能否為正方形?若能,求出t的值,若不能,請說明理由.
【答案】(1)①②③;(2)S=a(a>0);(3)①![]() ;②t=﹣2或1或4.
;②t=﹣2或1或4.
【解析】
(1)二次函數(shù)y=ax2﹣2ax﹣2的對稱軸為x=![]() =1,y=ax2﹣2ax﹣2=a(x2﹣2x)﹣2,即可求解;
=1,y=ax2﹣2ax﹣2=a(x2﹣2x)﹣2,即可求解;
(2)由S=S△BMD﹣S△AMD=![]() MD(OC﹣AC),即可求解;
MD(OC﹣AC),即可求解;
(3)①而x=1和x=m關(guān)于P(t,﹣2)中心對稱,所以P到這兩條對稱軸的距離相等,則1﹣t=t﹣m,m=2t﹣1,且:2t﹣1≤﹣2,即可求解;②分t≤1、t>1兩種情況求解即可.
解:(1)二次函數(shù)y=ax2﹣2ax﹣2的對稱軸為x=![]() =1,
=1,
當x=1時,y=﹣a﹣2;
y=ax2﹣2ax﹣2=a(x2﹣2x)﹣2,即當x=0或2時,拋物線過定點,即(0,﹣2)、(2,﹣2),
故答案為:①②③;
(2)由拋物線的頂點公式求得:頂點M(1,﹣a﹣2)
當x=1時,y=2×1﹣a=2﹣a,求得:D(1,2﹣a)
當y=0時,0=2x﹣a,x=![]() a,求得:A(a/2,0)
a,求得:A(a/2,0)
∴DM=2﹣a﹣(﹣a﹣2)=4,
S=S△BMD﹣S△AMD=![]() MD(OC﹣AC)=
MD(OC﹣AC)=![]() ×4×
×4×![]() a=a(a>0),
a=a(a>0),
(3)①當﹣2≤x≤1時,
C1的y的值都會隨x的增大而減小,而C1的對稱軸為x=1,
﹣2≤x≤1在對稱軸的左側(cè),C1開口向上,所以a>0;
同時C2的開口向下,而又要當﹣2≤x≤1時y的值都會隨x的增大而減小,
所以﹣2≤x≤1要在C2的對稱軸右側(cè),
令C2的對稱軸為x=m,則m≤﹣2,
而x=1和x=m關(guān)于P(t,﹣2)中心對稱,所以P到這兩條對稱軸的距離相等,
所以:1﹣t=t﹣m,m=2t﹣1,且:2t﹣1≤﹣2,即:![]() ;
;
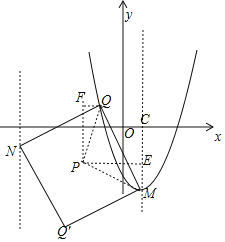
②當a=1時,M(1,﹣3),作PE⊥CM于E,將Rt△PME繞P旋轉(zhuǎn)180°,得到Rt△PQF,
則△MPQ為等腰直角三角形,因為N、Q′是中心對稱點,所以四邊形MQNQ′為正方形.
第一種情況,當t≤1時,
PE=PF=1﹣t,ME=QF=1,CE=2,
∴Q(t+1,﹣t﹣1),
把Q(t+1,﹣t﹣1)代入y=x2﹣2x﹣2
﹣t﹣1=(t+1)2﹣2(t+1)﹣2,
t2+t﹣2=0,
解得:t1=1,t2=﹣2;
第二種情況,當t>1時,
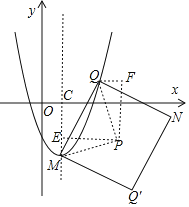
PE=PE=t﹣1,ME=QF=1,CE=2,
∴Q(t﹣1,t﹣3)代入:y=x2﹣2x﹣2,
t﹣3=(t﹣1)2﹣2(t﹣1)﹣2,
t2﹣5t+4=0,
解得:t1=1 (舍去),t2=4
綜上:t=﹣2或1或4.


科目:初中數(shù)學 來源: 題型:
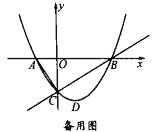
【題目】已知在平面直角坐標系中,拋物線![]() 與
與![]() 軸交于
軸交于![]() 兩點(點
兩點(點![]() 在點
在點![]() 左側(cè)),與
左側(cè)),與![]() 軸交于點
軸交于點![]() ,頂點為
,頂點為![]() .
.
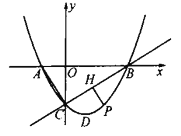
(1)如圖,直線![]() 下方拋物線上的一個動點
下方拋物線上的一個動點![]() (不與點
(不與點![]() 重合),過點
重合),過點![]() 作
作![]() 于點
于點![]() ,當
,當![]() 最大時,點
最大時,點![]() 為線段
為線段![]() 一點(不與點
一點(不與點![]() 重合),當
重合),當![]() 的值最小時,求點
的值最小時,求點![]() 的坐標;
的坐標;
(2)將![]() 沿直線
沿直線![]() 翻折得
翻折得![]() ,再將
,再將![]() 繞著點
繞著點![]() 順時針旋轉(zhuǎn)
順時針旋轉(zhuǎn)![]() 得
得![]() ,在旋轉(zhuǎn)過程中直線
,在旋轉(zhuǎn)過程中直線![]() 與直線
與直線![]() 相交于點
相交于點![]() ,與
,與![]() 軸相交于點
軸相交于點![]() ,當
,當![]() 是等腰三角形時,求
是等腰三角形時,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】閱讀下列材料:數(shù)學課上,老師出示了這樣一個問題:
如圖1,在等邊![]() 中,點
中,點![]() 、
、![]() 在
在![]() 上,且
上,且![]() ,直線
,直線![]() 交
交![]() 于
于![]() 點,交
點,交![]() 延長線于
延長線于![]() 點,且
點,且![]() ,探究線段
,探究線段![]() 之間的數(shù)量關(guān)系,并證明.
之間的數(shù)量關(guān)系,并證明.
某學習小組的同學經(jīng)過思考,交流了自己的想法:
小明:“通過觀察和度量,發(fā)現(xiàn)![]() 與
與![]() 存在某種數(shù)量關(guān)系”;
存在某種數(shù)量關(guān)系”;
小強:“通過觀察和度量,發(fā)現(xiàn)圖1中有一條線段與![]() 相等”;
相等”;
小偉:“通過構(gòu)造三角形,證明三角形全等,進而可以得到線段![]() 之間的數(shù)量關(guān)系”.
之間的數(shù)量關(guān)系”.
……
老師:“保留原題條件,再過點![]() 作
作![]() 交
交![]() 于
于![]() 與
與![]() 相交于點
相交于點![]() (如圖2)如果給出
(如圖2)如果給出![]() 的值,那么可以求出
的值,那么可以求出![]() 的值”.
的值”.
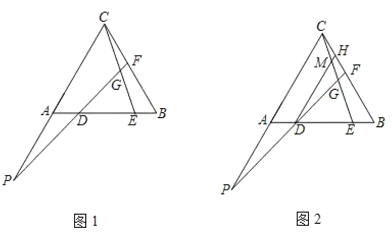
請回答:
(1)在圖1中找出![]() 與
與![]() 數(shù)量關(guān)系,并證明;
數(shù)量關(guān)系,并證明;
(2)在圖1中找出與線段![]() 相等的線段,并證明;
相等的線段,并證明;
(3)探究線段![]() 之間的數(shù)量關(guān)系,并證明;
之間的數(shù)量關(guān)系,并證明;
(4)若![]() ,求
,求![]() 的值(用含
的值(用含![]() 的代數(shù)式表示).
的代數(shù)式表示).
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】小文同學統(tǒng)計了某棟居民樓中全體居民每周使用手機支付的次數(shù),并繪制了直方圖.根據(jù)圖中信息,下列說法錯誤的是( )
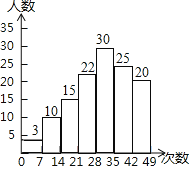
A.這棟居民樓共有居民125人
B.每周使用手機支付次數(shù)為28~35次的人數(shù)最多
C.有的人每周使用手機支付的次數(shù)在35~42次
D.每周使用手機支付不超過21次的有15人
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】為積極響應“弘揚傳統(tǒng)文化”的號召,某學校倡導全校1200名學生進行經(jīng)典詩詞誦背活動,并在活動之后舉辦經(jīng)典詩詞大賽,為了解本次系列活動的持續(xù)效果,學校團委在活動啟動之初,隨機抽取部分學生調(diào)查“一周詩詞誦背數(shù)量”,根調(diào)查結(jié)果繪制成的統(tǒng)計圖(部分)如圖所示.
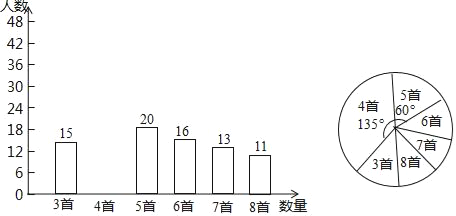
大賽結(jié)束后一個月,再次抽查這部分學生“一周詩詞誦背數(shù)量”,繪制成統(tǒng)計表
一周詩詞誦背數(shù)量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人數(shù) | 10 | 10 | 15 | 40 | 25 | 20 |
請根據(jù)調(diào)查的信息
(1)活動啟動之初學生“一周詩詞誦背數(shù)量”的中位數(shù)為 ;
(2)估計大賽后一個月該校學生一周詩詞誦背6首(含6首)以上的人數(shù);
(3)選擇適當?shù)慕y(tǒng)計量,從兩個不同的角度分析兩次調(diào)查的相關(guān)數(shù)據(jù),評價該校經(jīng)典詩詞誦背系列活動的效果.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】正方形![]() 的邊長為3,點
的邊長為3,點![]() ,
,![]() 分別在射線
分別在射線![]() ,
,![]() 上運動,且
上運動,且![]() .連接
.連接![]() ,作
,作![]() 所在直線于點
所在直線于點![]() ,連接
,連接![]() .
.
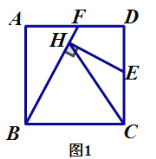

(1)如圖1,若點![]() 是
是![]() 的中點,
的中點,![]() 與
與![]() 之間的數(shù)量關(guān)系是______;
之間的數(shù)量關(guān)系是______;
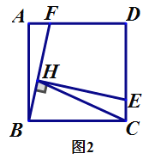
(2)如圖2,當點![]() 在
在![]() 邊上且不是
邊上且不是![]() 的中點時,(1)中的結(jié)論是否成立?若成立給出證明;若不成立,說明理由;
的中點時,(1)中的結(jié)論是否成立?若成立給出證明;若不成立,說明理由;
(3)如圖3,當點![]() ,
,![]() 分別在射線
分別在射線![]() ,
,![]() 上運動時,連接
上運動時,連接![]() ,過點
,過點![]() 作直線
作直線![]() 的垂線,交直線
的垂線,交直線![]() 于點
于點![]() ,連接
,連接![]() ,求線段
,求線段![]() 長的最大值.
長的最大值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() 為
為![]() 上一動點,
上一動點,![]() 點從
點從![]() 點以1個單位/秒的速度向
點以1個單位/秒的速度向![]() 點運動,遠動到
點運動,遠動到![]() 點即停止,經(jīng)過
點即停止,經(jīng)過![]() 點作
點作![]() ,交
,交![]() 于點
于點![]() ,以
,以![]() 為一邊在
為一邊在![]() 一側(cè)作正方形
一側(cè)作正方形![]() ,在
,在![]() 點運動過程中,設正方形
點運動過程中,設正方形![]() 與
與![]() 的重疊面積為
的重疊面積為![]() ,運動時間為
,運動時間為![]() 秒,如圖2是
秒,如圖2是![]() 與
與![]() 的函數(shù)圖象.
的函數(shù)圖象.
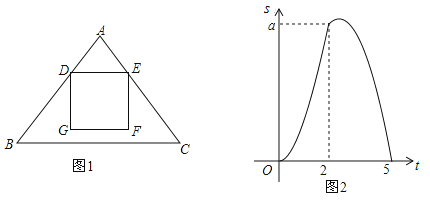
(1)求![]() 的長;
的長;
(2)求![]() 的值;
的值;
(3)求![]() 與
與![]() 的函數(shù)關(guān)系式.
的函數(shù)關(guān)系式.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知:關(guān)于x的方程![]()
(1)求證:m取任何值時,方程總有實根.
(2)若二次函數(shù)![]() 的圖像關(guān)于y軸對稱.
的圖像關(guān)于y軸對稱.
a、求二次函數(shù)![]() 的解析式
的解析式
b、已知一次函數(shù)![]() ,證明:在實數(shù)范圍內(nèi),對于同一x值,這兩個函數(shù)所對應的函數(shù)值
,證明:在實數(shù)范圍內(nèi),對于同一x值,這兩個函數(shù)所對應的函數(shù)值![]() 均成立.
均成立.
(3)在(2)的條件下,若二次函數(shù)![]() 的象經(jīng)過(-5,0),且在實數(shù)范圍內(nèi),對于x的同一個值,這三個函數(shù)所對應的函數(shù)值
的象經(jīng)過(-5,0),且在實數(shù)范圍內(nèi),對于x的同一個值,這三個函數(shù)所對應的函數(shù)值![]() 均成立,求二次函數(shù)
均成立,求二次函數(shù)![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
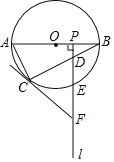
【題目】如圖,![]() 是
是![]() 的直徑,點
的直徑,點![]() 為
為![]() 上一點,點
上一點,點![]() 是半徑
是半徑![]() 上一動點(不與
上一動點(不與![]() ,
,![]() 重合),過點
重合),過點![]() 作射線
作射線![]() ,分別交弦
,分別交弦![]() ,
,![]() 于
于![]() ,
,![]() 兩點,在射線
兩點,在射線![]() 上取點
上取點![]() ,使
,使![]() .
.
(1)求證:![]() 是
是![]() 的切線;
的切線;
(2)當點![]() 是
是![]() 的中點時,
的中點時,
①若![]() ,判斷以
,判斷以![]() ,
,![]() ,
,![]() ,
,![]() 為頂點的四邊形是什么特殊四邊形,并說明理由;
為頂點的四邊形是什么特殊四邊形,并說明理由;
②若![]() ,且
,且![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com