
【題目】如圖, ![]() 是
是 ![]() 的中線,
的中線, ![]() 是線段
是線段 ![]() 上一點(diǎn)(不與點(diǎn)
上一點(diǎn)(不與點(diǎn) ![]() 重合).
重合). ![]() 交
交 ![]() 于點(diǎn)
于點(diǎn) ![]() ,
, ![]() ,連結(jié)
,連結(jié) ![]() .
.
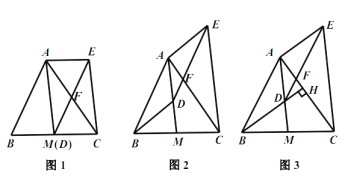
(1)如圖1,當(dāng)點(diǎn)![]() 與
與![]() 重合時(shí),求證:四邊形
重合時(shí),求證:四邊形![]() 是平行四邊形
是平行四邊形
(2)如圖2,當(dāng)點(diǎn)![]() 不與
不與![]() 重合時(shí),(1)中的結(jié)論還成立嗎?請說明理由.
重合時(shí),(1)中的結(jié)論還成立嗎?請說明理由.
(3)如圖3,延長![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() ,若
,若![]() ,且
,且![]() .
.
①求![]() 的度數(shù);
的度數(shù);
②當(dāng)![]() ,
,![]() 時(shí),求
時(shí),求 ![]() 的長.
的長.
【答案】(1)證明見解析(2)成立,理由見解析;(3)①30°.②1+![]() .
.
【解析】
試題(1)只要證明AE=BM,AE∥BM即可解決問題;
(2)成立.如圖2中,過點(diǎn)M作MG∥DE交CE于G.由四邊形DMGE是平行四邊形,推出ED=GM,且ED∥GM,由(1)可知AB=GM,AB∥GM,可知AB∥DE,AB=DE,即可推出四邊形ABDE是平行四邊形;
(3)①如圖3中,取線段HC的中點(diǎn)I,連接MI,只要證明MI=![]() AM,MI⊥AC,即可解決問題;
AM,MI⊥AC,即可解決問題;
②設(shè)DH=x,則AH=![]() x,AD=2x,推出AM=4+2x,BH=4+2x,由四邊形ABDE是平行四邊形,推出DF∥AB,推出
x,AD=2x,推出AM=4+2x,BH=4+2x,由四邊形ABDE是平行四邊形,推出DF∥AB,推出![]() ,可得
,可得![]() ,解方程即可;
,解方程即可;
試題解析:(1)證明:如圖1中,

∵DE∥AB,
∴∠EDC=∠ABM,
∵CE∥AM,
∴∠ECD=∠ADB,
∵AM是△ABC的中線,且D與M重合,
∴BD=DC,
∴△ABD≌△EDC,
∴AB=ED,∵AB∥ED,
∴四邊形ABDE是平行四邊形.
(2)結(jié)論:成立.理由如下:
如圖2中,過點(diǎn)M作MG∥DE交CE于G.
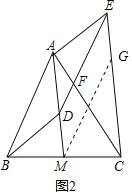
∵CE∥AM,
∴四邊形DMGE是平行四邊形,
∴ED=GM,且ED∥GM,
由(1)可知AB=GM,AB∥GM,
∴AB∥DE,AB=DE,
∴四邊形ABDE是平行四邊形.
(3)①如圖3中,取線段HC的中點(diǎn)I,連接MI,
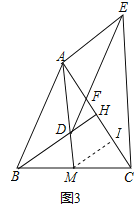
∵BM=MC,
∴MI是△BHC的中位線,
∴∥BH,MI=![]() BH,
BH,
∵BH⊥AC,且BH=AM.
∴MI=![]() AM,MI⊥AC,
AM,MI⊥AC,
∴∠CAM=30°.
②設(shè)DH=x,則AH=![]() x,AD=2x,
x,AD=2x,
∴AM=4+2x,
∴BH=4+2x,
∵四邊形ABDE是平行四邊形,
∴DF∥AB,
∴![]() ,
,
∴![]() ,
,
解得x=1+![]() 或1-
或1-![]() (舍棄),
(舍棄),
∴DH=1+![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,AB是⊙O的直徑,C是⊙O上一點(diǎn),D在AB的延長線上,且∠BCD=∠A.
(1)求證:CD是⊙O的切線;
(2)若⊙O的半徑為3,CD=4,求BD的長.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知,二次函數(shù)的解析式為![]() .
.
(1)它與![]() 軸的交點(diǎn)的坐標(biāo)為________,頂點(diǎn)坐標(biāo)為________;
軸的交點(diǎn)的坐標(biāo)為________,頂點(diǎn)坐標(biāo)為________;
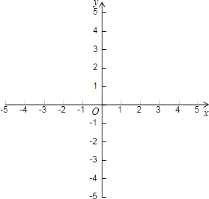
(2)在給定的坐標(biāo)系中畫出這個二次函數(shù)的圖象,并求出拋物線與坐標(biāo)軸的交點(diǎn)所組成的三角形的面積;
(3)根據(jù)圖象直接寫出拋物線在![]() 范圍內(nèi),函數(shù)值
范圍內(nèi),函數(shù)值![]() 的取值范圍是________.
的取值范圍是________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
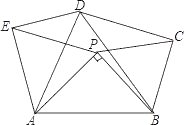
【題目】如圖,△APB中,AB=2,∠APB=90°,在AB的同側(cè)作正△ABD、正△APE和正△BPC,則四邊形PCDE面積的最大值是__.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
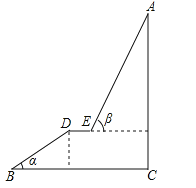
【題目】如圖,A為某旅游景區(qū)的最佳觀景點(diǎn),游客可從B處乘坐纜車先到達(dá)小觀景平臺DE觀景,然后再由E處繼續(xù)乘坐纜車到達(dá)A處,返程時(shí)從A處乘坐升降電梯直接到達(dá)C處,已知:AC⊥BC于C,DE∥BC,BC=110米,DE=9米,BD=60米,α=32°,β=68°,求AC的高度.(參考數(shù)據(jù):sin32°≈0.53;cos32°≈0.85;tan32°≈0.62;sin68°≈0.93;cos68°≈0.37;tan68°≈2.48)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
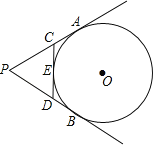
【題目】如圖,PA,PB切⊙O于A、B兩點(diǎn),CD切⊙O于點(diǎn)E,交PA,PB于C,D.若⊙O的半徑為r,△PCD的周長等于3r,則tan∠APB的值是__________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
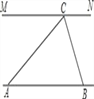
【題目】為解決江北學(xué)校學(xué)生上學(xué)過河難的問題,鄉(xiāng)政府決定修建一座橋,建橋過程中需測量河的寬度(即兩平行
河岸AB與MN之間的距離).在測量時(shí),選定河對岸MN上的點(diǎn)C處為橋的一端,在河岸點(diǎn)A處,測得∠CAB=30°,
沿河岸AB前行30米后到達(dá)B處,在B處測得∠CBA=60°,請你根據(jù)以上測量數(shù)據(jù)求出河的寬度.(參考數(shù)據(jù): ![]() ≈1.41,
≈1.41, ![]() ≈1.73,結(jié)果保留整數(shù))
≈1.73,結(jié)果保留整數(shù))
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,△ADE的頂點(diǎn)D,E分別在BC,AC上,且∠DAE=90°,AD=AE.若∠C+∠BAC=145°,則∠EDC的度數(shù)為( )
A. 17.5° B. 12.5° C. 12° D. 10°
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com