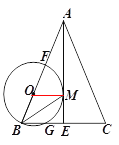
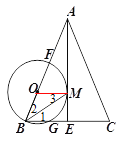
【題目】如圖，在△ABC中,AB=AC,AE是BC邊上的高線，BM平分∠ABC交AE于點M，經(jīng)過B，M 兩點的⊙O交BC于點G，交AB于點F ，F(xiàn)B為⊙O的直徑．
（1）求證：AM是⊙O的切線
（2）當BE=3，cosC=
時，求⊙O的半徑．
【答案】(1)見解析；(2) 
【解析】分析：(1)連結(jié)
根據(jù)BM平分∠ABC，得到
根據(jù)
，得到
根據(jù)等量代換得到證明OM∥BC，AE是BC邊上的高線，得到
，即可證明.
根據(jù)cosC=
=
,求出
的長度，根據(jù)
, cos∠AOM = cosC=,
得到AO=
, AB=+OB=
,求解即可.
詳解：(1)連結(jié)
∵BM平分∠ABC，
∴ 又
∴
∴ OM∥BC，
AE是BC邊上的高線
∴
∴
∴AM是⊙O的切線
（2）∵
,
∴
,
∴E是BC中點,∴
,
∵cosC==,
∴
∵OM∥ BC，
,
∴, ∴
又
∴
在
中，cos∠AOM = cosC=,
∴AO=,
AB=+OB=,
而
∴=
,
OM=,
∴⊙O的半徑是.
閱讀快車系列答案科目：初中數(shù)學 來源： 題型：
【題目】有理數(shù)a、b在數(shù)軸上的位置如圖所示，且|a|＜|b|，下列各式中正確的個數(shù)是（ ）
①a+b＜0；②b﹣a＞0；③
；④3a﹣b＞0；⑤﹣a﹣b＞0．
A. 2個B. 3個C. 4個D. 5個
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】下列命題：①全等三角形的對應邊上的中線，高線，對應角的平分線對應相等；②兩邊和其中一邊上的中線（或第三邊上的中線）對應相等的兩個三角形全等；③兩角和其中一角的角平分線（或第三角的角平分線）對應相等的兩個三角形全等；④兩邊和其中一邊上的高線（或第三邊上的高線）對應相等的兩個三角形全等．其中正確命題有________．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】若拋物線L1：y=ax2+bx+c(a，b，c是常數(shù)，abc≠0)與直線L2都經(jīng)過y軸上的一點P，且拋物線L1與頂點Q在直線L2上，則稱此直線L2與該拋物線L1具有“一帶一路”關系，此時，直線L2叫做拋物線L1的“帶線”，拋物線L1叫做直L2的“路線”.
(1) 若直線y=mx+1與拋物線y=x2-2x+n具有“一帶一路”關系，則m+n=_______.
(2) 若某“路線”L1的頂點在反比例函數(shù)
的圖像上，它的“帶線” L2的解析式為y=2x-4，則此“路線”L的解析式為：_____________.
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
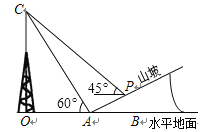
【題目】如圖所示，某人在山坡坡腳A處測得電視塔尖點C 的仰角為60°，沿山坡向上走到P處再測得C的仰角為45°，已知OA＝200米，山坡坡度為
（即tan∠PAB＝
），且O、A、B在同一條直線上，求電視塔OC的高度以及此人所在位置點P的垂直高度．（測傾器的高度忽略不計，結(jié)果保留根號）
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】根據(jù)材料，解答問題
如圖，數(shù)軸上有點
，對應的數(shù)分別是6，-4，4，-1，則
兩點間的距離為
；
兩點間的距離為
；
兩點間的距離為
；由此，若數(shù)軸上任意兩點
分別表示的數(shù)是
，則
兩點間的距離可表示為
．反之，表示有理數(shù)
在數(shù)軸上的對應點之間的距離，稱之為絕對值的幾何意義．
問題應用1：
（1）如果表示-1的點
和表示
的點
之間的距離是2，則點對應的的值為___________；
（2）方程
的解
____________；
（3）方程
的解______________ ；
問題應用2：
如圖，若數(shù)軸上表示
的點為
.
（4）
的幾何意義是數(shù)軸上_____________，當
__________，的值最小是____________；
（5）
的幾何意義是數(shù)軸上_______，的最小值是__________，此時點在數(shù)軸上應位于__________上；
（6）根據(jù)以上推理方法可求
的最小值是___________，此時__________．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
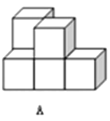
【題目】在桌面上,有若干個完全相同的小正方體堆成的一個幾何體
,如圖所示．
(1)請畫出這個幾何體的三視圖．
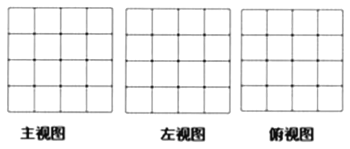
(2)若將此幾何體的表面噴上紅漆(放在桌面上的一面不噴),則三個面上是紅色的小正方體有 個．
(3)若現(xiàn)在你的手頭還有一些相同的小正方體可添放在幾何體上,要保持主視圖和左視圖不變,則最多可以添加___個小正方體．
(4)若另一個幾何體
與幾何體的主視圖和左視圖相同,而小正方體個數(shù)則比幾何體多1個,請在圖2中畫出幾何體的俯視圖中的任意兩種．
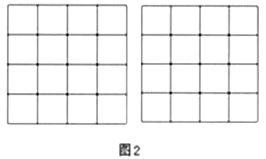
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】如圖1，在矩形ABCD中，AD=4，AB=2
，將矩形ABCD繞點A逆時針旋轉(zhuǎn)α（0＜α＜90°）得到矩形AEFG．延長CB與EF交于點H．
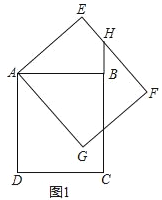
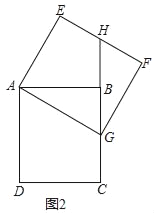
（1）求證：BH=EH；
（2）如圖2，當點G落在線段BC上時，求點B經(jīng)過的路徑長．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】[閱讀理解]射線
是
內(nèi)部的一條射線，若
則我們稱射線是射線
的伴隨線．
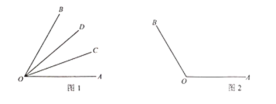
例如，如圖1，
，則
，稱射線是射線的伴隨線：同時，由于
，稱射線
是射線
的伴隨線．
[知識運用]
（1）如圖2，
，射線
是射線的伴隨線，則
，若的度數(shù)是
，射線
是射線的伴隨線，射線是的平分線，則
的度數(shù)是 ．（用含的代數(shù)式表示）
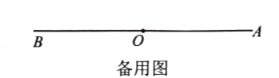
（2）如圖，如
，射線與射線重合，并繞點
以每秒
的速度逆時針旋轉(zhuǎn)，射線與射線重合，并繞點以每秒
的速度順時針旋轉(zhuǎn)，當射線與射線重合時，運動停止，現(xiàn)在兩射線同時開始旋轉(zhuǎn)．
①是否存在某個時刻
（秒），使得
的度數(shù)是
，若存在，求出的值，若不存在，請說明理由；
②當為多少秒時，射線
中恰好有一條射線是其余兩條射線的伴隨線．
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com