
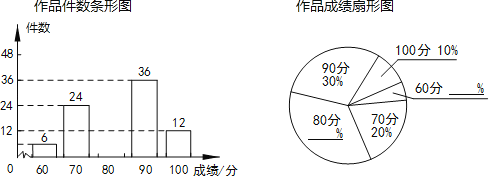
【題目】3月5日是學雷鋒日,某校組織了以“向雷鋒同志學習”為主題的小報制作比賽,評分結果只有60,70,80,90,100五種.現從中隨機抽取部分作品,對其份數及成績進行整理,制成如下兩幅不完整的統計圖.根據以下信息,解答下列問題:
(1)求本次抽取了多少份作品,并補全兩幅統計圖;
(2)已知該校收到參賽作品共1200份,請估計該校學生比賽成績達到90分以上(含90分)的作品有多少份?
【答案】(1)120份作品 (2) 480份
【解析】
試題(1) 只要找出部分的具體量以及對應的百分數就可以求出總量,選取100分的,有12份,占總數的10%,所以本次抽取的作品數位:12÷10%=120(份);
由總數推斷出60分的有6份,占了總數的6÷120=5%(在圖中表示出來);
80分的分數有120-(6+24+36+12)=42(份),占總人數42÷120=35﹪, 或者用1-(10%+30%+20%+5%)=35%(在圖中表示出來)
(2)90分以上的包括90和100,總共占了(30﹪+10﹪),那么1200份中達到的有:1200×(30﹪+10﹪)=480份
∴該校學生比賽成績達到90分以上(含90分)的作品有480份.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
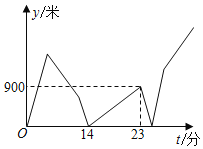
【題目】已知A、B、C三地順次在同一直線上,甲、乙兩人均騎車從A地出發,向C地勻速行駛.甲比乙早出發5分鐘,甲到達B地并休息了2分鐘后,乙追上了甲.甲、乙同時從B地以各自原速繼續向C地行駛.當乙到達C地后,乙立即掉頭并提速為原速的![]() 倍按原路返回A地,而甲也立即提速為原速的
倍按原路返回A地,而甲也立即提速為原速的![]() 倍繼續向C地行駛,到達C地就停止.若甲、乙間的距離y(米)與甲出發的時間t(分)之間的函數關系如圖所示,則當甲到達C地時,乙距A地_____米.
倍繼續向C地行駛,到達C地就停止.若甲、乙間的距離y(米)與甲出發的時間t(分)之間的函數關系如圖所示,則當甲到達C地時,乙距A地_____米.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】鐘南山院士談到防護新型冠狀病毒肺炎時說:“我們需要重視防護,但也不必恐慌,盡量少去人員密集的場所,出門戴口罩,在室內注意通風,勤洗手,多運動,少熬夜.”某社區為了加強社區居民對新型冠狀病毒肺炎防護知識的了解,通過微信群宣傳新型冠狀病毒肺炎的防護知識,并鼓勵社區居民在線參與作答《2020年新型冠狀病毒防治全國統一考試(全國卷)》試卷(滿分100分),社區管理員隨機從有400人的某小區抽取40名人員的答卷成績,并對他們的成績(單位:分)統計如下:
85 | 80 | 95 | 100 | 90 | 95 | 85 | 65 | 75 | 85 |
90 | 90 | 70 | 90 | 100 | 80 | 80 | 90 | 95 | 75 |
80 | 60 | 80 | 95 | 85 | 100 | 90 | 85 | 85 | 80 |
95 | 75 | 80 | 90 | 70 | 80 | 95 | 75 | 100 | 90 |
根據數據繪制了如下的表格和統計圖:
等級 | 成績( | 頻率 | 頻率 |
|
| 10 | 0.25 |
|
|
| |
|
| 12 | 0.3 |
|
|
| |
合計 | 40 | 1 | |
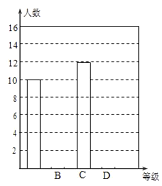
根據上面提供的信息,回答下列問題:
(1)統計表中的![]() ,
,![]() ;
;
(2)請補全條形統計圖;
(3)根據抽樣調查結果,請估計該小區答題成績為“![]() 級”的有多少人?
級”的有多少人?
(4)該社區有2名男管理員和2名女管理員,現從中隨機挑選2名管理員參加“社區防控”宣傳活動,請用樹狀圖法或列表法求出恰好選中“1男1女”的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
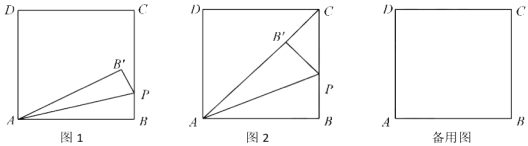
【題目】如圖1,在矩形![]() 中,BC=3,動點
中,BC=3,動點![]() 從
從![]() 出發,以每秒1個單位的速度,沿射線
出發,以每秒1個單位的速度,沿射線![]() 方向移動,作
方向移動,作![]() 關于直線
關于直線![]() 的對稱
的對稱![]() ,設點
,設點![]() 的運動時間為
的運動時間為![]()
(1)若![]()
①如圖2,當點B’落在AC上時,顯然△PCB’是直角三角形,求此時t的值
②是否存在異于圖2的時刻,使得△PCB’是直角三角形?若存在,請直接寫出所有符合題意的t的值?若不存在,請說明理由
(2)當P點不與C點重合時,若直線PB’與直線CD相交于點M,且當t<3時存在某一時刻有結論∠PAM=45°成立,試探究:對于t>3的任意時刻,結論∠PAM=45°是否總是成立?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,拋物線y=﹣x2+mx+n交x軸于點A(﹣2,0)和點B,交y軸于點C(0,2).
(1)求拋物線的函數表達式;
(2)若點M在拋物線上,且S△AOM=2S△BOC,求點M的坐標;
(3)如圖2,設點N是線段AC上的一動點,作DN⊥x軸,交拋物線于點D,求線段DN長度的最大值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=﹣x2+2x+3,截取該函數圖象在0≤x≤4間的部分記為圖象G,設經過點(0,t)且平行于x軸的直線為l,將圖象G在直線l下方的部分沿直線l翻折,圖象G在直線上方的部分不變,得到一個新函數的圖象M,若函數M的最大值與最小值的差不大于5,則t的取值范圍是( )
A.﹣1≤t≤0B.﹣1≤t![]() C.
C.![]() D.t≤﹣1或t≥0
D.t≤﹣1或t≥0
查看答案和解析>>
科目:初中數學 來源: 題型:
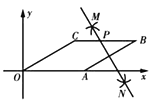
【題目】如圖,在菱形![]() 中,
中,![]() ,
,![]() ,以
,以![]() 為坐標原點,以
為坐標原點,以![]() 所在的直線為
所在的直線為![]() 軸建立平面直角坐標系,如圖.按以下步驟作圖:①分別以點
軸建立平面直角坐標系,如圖.按以下步驟作圖:①分別以點![]() ,
,![]() 為圓心,以大于
為圓心,以大于![]() 的長為半徑作弧,兩弧相交于點
的長為半徑作弧,兩弧相交于點![]() ,
,![]() ;②作直線
;②作直線![]() 交
交![]() 于點
于點![]() .則點
.則點![]() 的坐標為( )
的坐標為( )
A.![]() B.
B.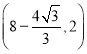 C.
C.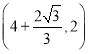 D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,菱形ABCD中,AB=10,連接BD,點P是射線BC上一點(不與點B重合),AP與對角線BD交于點E,連接EC.
(1)求證:AE=CE;
(2)若sin∠ABD=![]() ,當點P在線段BC上時,若BP=4,求△PEC的面積;
,當點P在線段BC上時,若BP=4,求△PEC的面積;
(3)若∠ABC=45°,當點P在線段BC的延長線上時,請直接寫出△PEC是等腰三角形時BP的長.
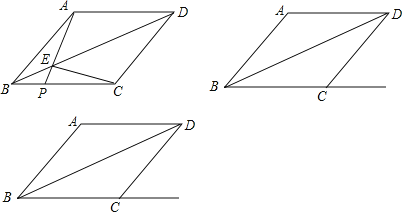
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com