
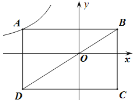
【題目】如圖,在平面直角坐標系中,矩形ABCD的對角線BD經過坐標原點O,矩形的邊分別平行于坐標軸,點A在函數![]() (
(![]() ≠0,
≠0,![]() <0)的圖象上,點C的坐標為(2,
<0)的圖象上,點C的坐標為(2,![]() ),則
),則![]() 的值為( )
的值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:初中數學 來源: 題型:
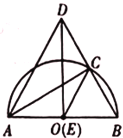
【題目】如圖,已知![]() ,以
,以![]() 為直徑作半圓
為直徑作半圓![]() ,半徑
,半徑![]() 繞點
繞點![]() 順時針旋轉得到
順時針旋轉得到![]() ,點
,點![]() 的對應點為
的對應點為![]() ,當點
,當點![]() 與點
與點![]() 重合時停止.連接
重合時停止.連接![]() 并延長到點
并延長到點![]() ,使得
,使得![]() ,過點
,過點![]() 作
作![]() 于點
于點![]() ,連接
,連接![]() ,
,![]() .
.
(1)![]() ______;
______;
(2)如圖,當點![]() 與點
與點![]() 重合時,判斷
重合時,判斷![]() 的形狀,并說明理由;
的形狀,并說明理由;
(3)如圖,當![]() 時,求
時,求![]() 的長;
的長;

(4)如圖,若點![]() 是線段
是線段![]() 上一點,連接
上一點,連接![]() ,當
,當![]() 與半圓
與半圓![]() 相切時,直接寫出直線
相切時,直接寫出直線![]() 與
與![]() 的位置關系.
的位置關系.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在平面直角坐標系xOy中,點A(0,2),正方形OABC的頂點B在函數![]() (k ≠ 0,x<0) 的圖象上,直線
(k ≠ 0,x<0) 的圖象上,直線![]() :
:![]() 與函數
與函數![]() (k ≠ 0,x<0) 的圖象交于點D,與x軸交于點E.
(k ≠ 0,x<0) 的圖象交于點D,與x軸交于點E.
(1)求k的值;
(2)橫、縱坐標都是整數的點叫做整點.
①當一次函數![]() 的圖象經過點A時,直接寫出△DCE內的整點的坐標;
的圖象經過點A時,直接寫出△DCE內的整點的坐標;
②若△DCE內的整點個數恰有6個,結合圖象,求b的取值范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,關于x的二次函數y=ax2﹣2ax(a>0)的頂點為C,與x軸交于點O、A,關于x的一次函數y=﹣ax(a>0).
(1)試說明點C在一次函數的圖象上;
(2)若兩個點(k,y1)、(k+2,y2)(k≠0,±2)都在二次函數的圖象上,是否存在整數k,滿足![]() ?如果存在,請求出k的值;如果不存在,請說明理由;
?如果存在,請求出k的值;如果不存在,請說明理由;
(3)若點E是二次函數圖象上一動點,E點的橫坐標是n,且﹣1≤n≤1,過點E作y軸的平行線,與一次函數圖象交于點F,當0<a≤2時,求線段EF的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】每年5月的第二個星期日即為母親節,“父母恩深重,恩憐無歇時”,許多市民喜歡在母親節為母親送花,感恩母親,祝福母親.今年節日前夕,某花店采購了一批鮮花禮盒,經分析上一年的銷售情況,發現該鮮花禮盒的該周銷售量y(盒)是銷售單價x(元)的一次函數,已知銷售單價為70元/盒時,銷售量為160盒;銷售單價為80元/盒時,銷售量為140盒.
(1)求該周銷售量y(盒)關于銷售單價x(元)的一次函數解析式;
(2)若按去年方式銷售,已知今年該鮮花禮盒的進價是每盒50元,商家要求該周至少要賣110盒,請你幫店長算一算,要完成商家的銷售任務,銷售單價不能超過多少元?
(3)在(2)的條件下,試確定銷售單價x為何值時,花店該周銷售鮮花禮盒獲得的利潤最大?并求出獲得的最大利潤.
查看答案和解析>>
科目:初中數學 來源: 題型:
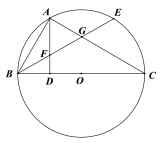
【題目】如圖,BC是⊙O的直徑,點A在⊙上,AD⊥BC,垂足為D,![]() ,BE分別交AD、AC與點F、G.
,BE分別交AD、AC與點F、G.
(1)證明:FA=FB.
(2)BD=DO=2,求弧EC的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
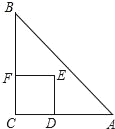
【題目】如圖,Rt△ABC中,AC=BC=2,正方形CDEF的頂點D、F分別在AC、BC邊上,設CD的長度為x,△ABC與正方形CDEF重疊部分的面積為y,則下列圖象中能表示y與x之間的函數關系的是( )
A. 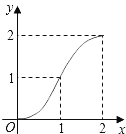 B.
B. 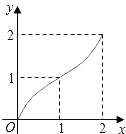
C. 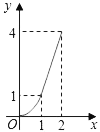 D.
D. 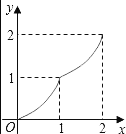
查看答案和解析>>
科目:初中數學 來源: 題型:
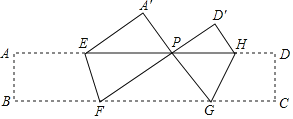
【題目】如圖,把矩形ABCD沿EF,GH折疊,使點B,C落在AD上同一點P處,∠FPG=90°,△A′EP的面積是8![]() ,△D′PH的面積是4
,△D′PH的面積是4![]() ,則矩形ABCD的面積等于_____.
,則矩形ABCD的面積等于_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
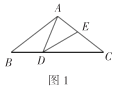
【題目】如圖1,在![]() 中,
中,![]() ,
,![]() ,點
,點![]() 是
是![]() 邊上的一個動點(不與
邊上的一個動點(不與![]() ,
,![]() 重合),以
重合),以![]() 為邊作
為邊作![]() ,交
,交![]() 邊于點
邊于點![]() .設
.設![]() ,
,![]() .今天我們將根據學習函數的經驗,研究函數值
.今天我們將根據學習函數的經驗,研究函數值![]() 隨自變量
隨自變量![]() 的變化而變化的規律.
的變化而變化的規律.
下面是某同學做的一部分研究結果,請你一起參與解答:
(1)自變量![]() 的取值范圍是 ;
的取值范圍是 ;
(2)通過計算,得到![]() 與
與![]() 的幾組值,如下表:
的幾組值,如下表:
| 0.5 | 1 | 1.5 | 2 | 3 | 4 | 4.5 | 5 | 5.5 |
| 3.3125 | 2.75 | 2.3125 | 2 | 2.3125 | 2.75 | 3.3125 |
請你補全表格;
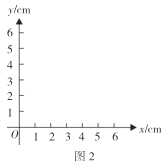
(3)在如圖2所示的平面直角坐標系中,畫出該函數的大致圖象;
(4)根據圖象,請寫出該函數的一條性質.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com