
【題目】已知:在![]() 中,
中,![]() ,點
,點![]() 在
在![]() 上,連結(jié)
上,連結(jié)![]() ,且
,且![]() .
.
(1)如圖1,求![]() 的度數(shù);
的度數(shù);
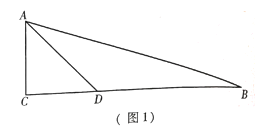
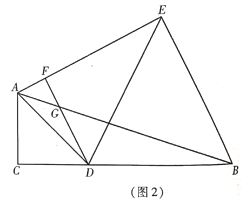
(2) 如圖2, 點![]() 在
在![]() 的垂直平分線上,連接
的垂直平分線上,連接![]() ,過點
,過點![]() 作
作![]() 于點
于點![]() ,
,![]() 交
交![]() 于點
于點![]() ,若
,若![]() ,
,![]() ,求證:
,求證: ![]() 是等腰直角三角形;
是等腰直角三角形;
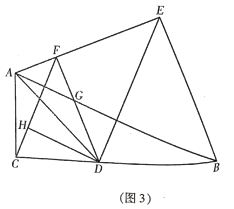
(3)如圖3,在(2)的條件下,連接![]() ,過點
,過點![]() 作
作 ![]() 交
交![]() 于點
于點![]() ,且
,且![]() ,若
,若![]() ,求
,求![]() 的長.
的長.
【答案】(1)![]() ;(2)證明見解析;(3)
;(2)證明見解析;(3)![]() .
.
【解析】
(1)根據(jù)已知推出![]() ,然后利用三角形外角的性質(zhì)有
,然后利用三角形外角的性質(zhì)有![]() ,則
,則![]() ,然后利用
,然后利用![]() 即可求解;
即可求解;
(2)由垂直平分線的性質(zhì)得到![]() ,從而有
,從而有![]() ,根據(jù)同位角相等,兩直線平行可得出
,根據(jù)同位角相等,兩直線平行可得出![]() ,進而得出
,進而得出![]() ,然后通過等量代換得出
,然后通過等量代換得出![]() ,所以
,所以![]() ,
,![]() ,則結(jié)論可證;
,則結(jié)論可證;
(3)首先證明![]() ,則有
,則有![]() ,
, ![]() ,
,![]() ,然后證明
,然后證明![]() 得出
得出![]() ,然后通過對角度的計算得出
,然后通過對角度的計算得出![]() ,
,![]() ,同理證明點
,同理證明點![]() 在
在![]() 的垂直平分線上 ,則有
的垂直平分線上 ,則有
![]() ,所以
,所以![]() ,最后通過證明
,最后通過證明![]() ,得出
,得出![]() ,則答案可解 .
,則答案可解 .
(1)![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(2)∵點 ![]() 在線段
在線段 ![]() 的垂直平分線上
的垂直平分線上
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
![]()
![]()
又![]()
∴![]()
![]()
![]()
![]() 是等腰直角三角形
是等腰直角三角形
(3)如圖 ,過![]() 作
作![]() 交
交 ![]() 的延長線于點
的延長線于點![]()
![]() 于點
于點![]() ,連接
,連接![]() ,令
,令![]() ,
,![]() 與
與![]() 的交點分別為點
的交點分別為點![]() ,
,![]() .
.
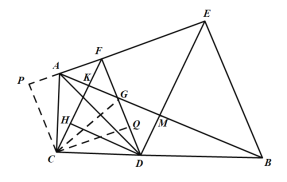
在四邊形![]() 中,
中,![]()
又![]()
![]()
又![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
又![]()
![]()
又![]()
![]()
![]()
又![]()
![]()
![]()
又![]()
![]()
![]()
![]()
![]()
![]()
![]()
∴點![]() 在
在![]() 的垂直平分線上
的垂直平分線上
同理點![]() 在
在![]() 的垂直平分線上
的垂直平分線上
![]()
![]()
![]()
![]()
![]()
![]()


 一線名師權(quán)威作業(yè)本系列答案
一線名師權(quán)威作業(yè)本系列答案科目:初中數(shù)學(xué) 來源: 題型:
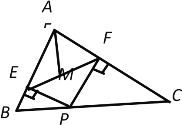
【題目】如圖,在△ABC中,AB=![]() ,AC=
,AC=![]() ,BC=
,BC=![]() ,P為邊BC上一動點,PE⊥AB于E,PF⊥AC于F,M為EF中點,則AM的最小值為__________.
,P為邊BC上一動點,PE⊥AB于E,PF⊥AC于F,M為EF中點,則AM的最小值為__________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
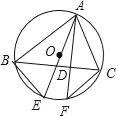
【題目】已知:如圖,△ABC內(nèi)接于⊙O,AF是⊙O的弦,AF⊥BC,垂足為D,點E為弧BF上一點,且BE=CF,
(1)求證:AE是⊙O的直徑;
(2)若∠ABC=∠EAC,AE=8,求AC的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() 為
為![]() 的中點,
的中點,![]() 、
、![]() 分別是
分別是![]() 、
、![]() (或它們的延長線)上的動點,且
(或它們的延長線)上的動點,且![]() .
.
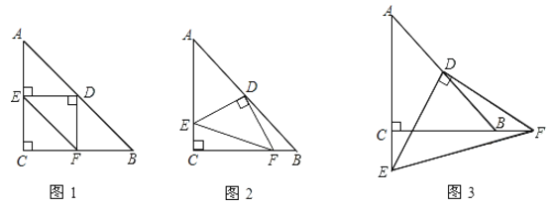
(1)當(dāng)![]() 時,如圖①,線段
時,如圖①,線段![]() 和線段
和線段![]() 的關(guān)系是:_________________;
的關(guān)系是:_________________;
(2)當(dāng)![]() 與
與![]() 不垂直時,如圖②,(1)的結(jié)論還成立嗎?若成立,請給予證明;若不成立,請說明理由;
不垂直時,如圖②,(1)的結(jié)論還成立嗎?若成立,請給予證明;若不成立,請說明理由;
(3)當(dāng)![]() 、
、![]() 運動到
運動到![]() 、
、![]() 的延長線時,如圖③,請直接寫出
的延長線時,如圖③,請直接寫出![]() 、
、![]() 、
、![]() 之間的關(guān)系.
之間的關(guān)系.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖是用4個全等的直角三角形與1個小正方形鑲嵌而成的正方形圖案,已知大正方形面積為49,小正方形面積為4,若用![]() ,
,![]() 表示直角三角形的兩直角邊(
表示直角三角形的兩直角邊(![]() ),下列四個說法:
),下列四個說法:

①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() .
.
其中說法正確的是 …………………………………………………………( )
A. ①② B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在一條筆直的公路上有![]() 兩地,甲,乙兩輛貨車都要從
兩地,甲,乙兩輛貨車都要從![]() 地送貨到
地送貨到![]() 地,甲車先從
地,甲車先從![]() 地出發(fā)勻速行駛,3小時后乙車從
地出發(fā)勻速行駛,3小時后乙車從![]() 地出發(fā),并沿同一路線勻速行駛,當(dāng)乙車到達
地出發(fā),并沿同一路線勻速行駛,當(dāng)乙車到達![]() 地后立刻按原速返回,在返回途中第二次與甲車相遇,甲車出發(fā)的時間記為
地后立刻按原速返回,在返回途中第二次與甲車相遇,甲車出發(fā)的時間記為![]() (小時),兩車之間的距離記為
(小時),兩車之間的距離記為![]() (千米),
(千米),![]() 與
與![]() 的函數(shù)關(guān)系如圖所示,則乙車第二次與甲車相遇是甲車距離
的函數(shù)關(guān)系如圖所示,則乙車第二次與甲車相遇是甲車距離![]() 地( )千米.
地( )千米.
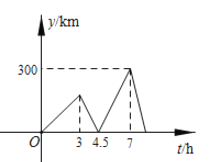
A.495B.505C.515D.525
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
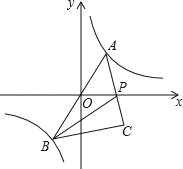
【題目】如圖,反比例函數(shù)y=![]() 的圖象上,點A是該圖象第一象限分支上的動點,連結(jié)AO并延長交另一支于點B,以AB為斜邊作等腰直角△ABC,頂點C在第四象限,AC與x軸交于點P,連結(jié)BP,在點A運動過程中,當(dāng)BP平分∠ABC時,點A的坐標(biāo)為_____.
的圖象上,點A是該圖象第一象限分支上的動點,連結(jié)AO并延長交另一支于點B,以AB為斜邊作等腰直角△ABC,頂點C在第四象限,AC與x軸交于點P,連結(jié)BP,在點A運動過程中,當(dāng)BP平分∠ABC時,點A的坐標(biāo)為_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在1、2、3、4、5這五個數(shù)中,先任意取一個數(shù)a,然后在余下的數(shù)中任意取出一個數(shù)b,組成一個點(a,b).求組成的點(a,b)恰好橫坐標(biāo)為偶數(shù)且縱坐標(biāo)為奇數(shù)的概率.(請用“畫樹狀圖”或“列表”等方法寫出分析過程)
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com