
【題目】如圖,點C是線段AB上一點,點M、N、P分別是線段AC,BC,AB的中點.
(1)若AB=10cm,則MN= cm;
(2)若AC=3cm,CP=1cm,求線段PN的長.
![]()
【答案】(1)5;(2)PN=![]() .
.
【解析】試題分析:(1)利用線段中點的性質得到MC,CN的長度,則MN=MC+CN;
(2)由已知條件可以求得AP=AC+CP=4cm,因為P是AB的中點,所以AB=2AP=8cm,BC=AB-AC=5cm,根據N為BC的中點,可求得CN,再根據PN=CN-CP即可求得PN的長.
試題解析:
(1)∵M、N分別是AC、BC的中點,
∴MC=![]() AC,CN=
AC,CN=![]() BC
BC
MN=MC+CN=![]() .
.
故填:5.
(2)∵AC=3,CP=1,
∴AP=AC+CP=4,
∵P是線段AB的中點,
∴AB=2AP=8
∴CB=AB﹣AC=5,
∵N是線段CB的中點,CN=![]() CB=
CB=![]() ,
,
∴PN=CN﹣CP=![]() .
.


科目:初中數學 來源: 題型:
【題目】下列說法不正確的是( )
A.直角三角形的兩個銳角互余
B.三角形任意兩邊之差小于第三邊
C.三角形的三條角平分線交于一點,這個點叫做三角形的重心
D.線段垂直平分線上的點到這條線段兩個端點的距離相等
查看答案和解析>>
科目:初中數學 來源: 題型:
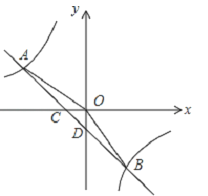
【題目】如圖,在平面直角坐標系中,一次函數的圖象與反比例函數的圖象交于第二、四象限內的A,B兩點,與x軸交于點C,與y軸交于點D,點B的坐標是(m,﹣4),連接AO,AO=5,sin∠AOC=![]() .
.
(1)求反比例函數的解析式;
(2)連接OB,求△AOB的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
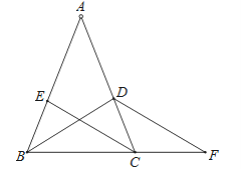
【題目】如圖:∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,∠DBF=∠F,那么EC與DF平行嗎?為什么?請完成下面的解題過程.
解:∵BD平分∠ABC,CE平分∠ACB ( 已知 )
∴DBC=![]() ∠________,∠ECB=
∠________,∠ECB=![]() ∠________
∠________
∵∠ABC=∠ACB (已知)
∴∠________=∠________.
∠________=∠________(已知)
∴∠F=∠________
∴EC∥DF________.
查看答案和解析>>
科目:初中數學 來源: 題型:
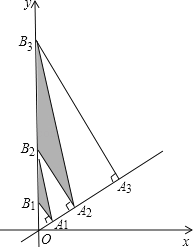
【題目】如圖,直線y=![]() x上有點A1,A2,A3,…An+1,且OA1=1,A1A2=2,A2A3=4,AnAn+1=2n分別過點A1,A2,A3,…An+1作直線y=
x上有點A1,A2,A3,…An+1,且OA1=1,A1A2=2,A2A3=4,AnAn+1=2n分別過點A1,A2,A3,…An+1作直線y=![]() x的垂線,交y軸于點B1,B2,B3,…Bn+1,依次連接A1B2,A2B3,A3B4,…AnBn+1,得到△A1B1B2,△A2B2B3,△A3B3B4,…,△AnBnBn+1,則△AnBnBn+1的面積為________.(用含有正整數n的式子表示)
x的垂線,交y軸于點B1,B2,B3,…Bn+1,依次連接A1B2,A2B3,A3B4,…AnBn+1,得到△A1B1B2,△A2B2B3,△A3B3B4,…,△AnBnBn+1,則△AnBnBn+1的面積為________.(用含有正整數n的式子表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
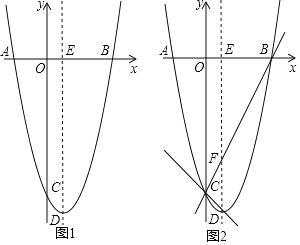
【題目】如圖,拋物線y=ax2﹣2x+c(a≠0)與x軸、y軸分別交于點A,B,C三點,已知點A(﹣2,0),點C(0,﹣8),點D是拋物線的頂點.
(1)求拋物線的解析式及頂點D的坐標;
(2)如圖1,拋物線的對稱軸與x軸交于點E,第四象限的拋物線上有一點P,將△EBP沿直線EP折疊,使點B的對應點B'落在拋物線的對稱軸上,求點P的坐標;
(3)如圖2,設BC交拋物線的對稱軸于點F,作直線CD,點M是直線CD上的動點,點N是平面內一點,當以點B,F,M,N為頂點的四邊形是菱形時,請直接寫出點M的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,點P的坐標為(0,﹣5),以P為圓心的圓與x軸相切,⊙P的弦AB(B點在A點右側)垂直于y軸,且AB=8,反比例函數![]() (k≠0)經過點B,則k=______.
(k≠0)經過點B,則k=______.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com