
【題目】甲、乙兩車從A地駛向B地,并以各自的速度勻速行駛,甲車比乙車早行駛2 h,并且甲車途中休息了0.5 h,如圖是甲、乙兩車行駛的路程y(km)與時間x(h)的函數圖象.
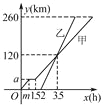
(1)求出圖中m和a的值.
(2)求出甲車行駛的路程y(km)與時間x(h)的函數關系式,并寫出相應的x的取值范圍.
(3)當乙車行駛多長時間時,兩車恰好相距50 km?
【答案】(1)m=1,a=40;(2)y=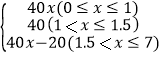 ;(3)
;(3)![]() h或
h或![]() h
h
【解析】試題分析:(1)根據“路程÷時間=速度”由函數圖象就可以求出甲的速度求出a的值和m的值;
(2)由分段函數當0≤x≤1,1<x≤1.5,1.5<x≤7由待定系數法就可以求出結論;
(3)先求出乙車行駛的路程y與時間x之間的解析式,由解析式之間的關系建立方程求出其解即可.
試題解析:(1)由圖知1.5-m=0.5 ∴m=1
![]() =
=![]() ∴a=40
∴a=40
(2)休息前,圖象過(1,40),所求函數為y=40x(0≤x≤1)
休息時,所求函數為y=40(1<x≤1.5)
休息后,圖象過(1.5,40),(3.5,120)
將坐標代入y=kx+b
![]() 解得
解得![]()
所求函數為y=40x-20(1.5<x≤7)
(3)設乙車行駛xh時,兩車恰好相距50km
相遇前,40(x+2-0.5)-80x=50
解得x=0.25h
相遇后,80x-40(x+2-0.5)=50
解得x=2.75h
答:乙車行駛0.25h或2.75h時,兩車恰好相距50km


 名師點撥卷系列答案
名師點撥卷系列答案 英才計劃期末調研系列答案
英才計劃期末調研系列答案科目:初中數學 來源: 題型:
【題目】如圖,C為射線AB上一點,AB=30,AC比BC的 ![]() 多5,P,Q兩點分別從A,B兩點同時出發.分別以2單位/秒和1單位/秒的速度在射線AB上沿AB方向運動,運動時間為t秒,M為BP的中點,N為QM的中點,以下結論: ①BC=2AC;②AB=4NQ;③當PB=
多5,P,Q兩點分別從A,B兩點同時出發.分別以2單位/秒和1單位/秒的速度在射線AB上沿AB方向運動,運動時間為t秒,M為BP的中點,N為QM的中點,以下結論: ①BC=2AC;②AB=4NQ;③當PB= ![]() BQ時,t=12,其中正確結論的個數是( )
BQ時,t=12,其中正確結論的個數是( )![]()
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,反比例函數的圖象經過點A、B,點A的坐標為(1,3),點B的縱坐標為1,點C的坐標為(2,0).
(1)求該反比例函數的表達式;
(2)求直線BC的表達式.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知直線y=![]() x與雙曲線y=
x與雙曲線y=![]() (k>0)交于A,B兩點,且點A的橫坐標為4.點C是雙曲線上一點,且縱坐標為8,則△AOC的面積為( )
(k>0)交于A,B兩點,且點A的橫坐標為4.點C是雙曲線上一點,且縱坐標為8,則△AOC的面積為( )

A. 8 B. 32 C. 10 D. 15
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知不在同一條直線上的三點P,M,N 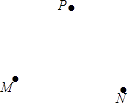
(1)畫射線NP;再畫直線MP;
(2)連接MN并延長MN至點R,使NR=MN;(保留作圖痕跡,不寫作圖過程)
(3)若∠PNR比∠PNM大100°,求∠PNR的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】先化簡再求值
(1)3a2﹣7a+[3a﹣2(a2﹣2a﹣1)],其中a=﹣2.
(2)已知A=3x2+2xy﹣5y2,B=2x2+xy﹣3y2.求:A﹣2B
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知∠AOB=α(90°<α<180°),∠COD在∠AOB的內部,OM平分∠AOC,ON平分∠BOD. 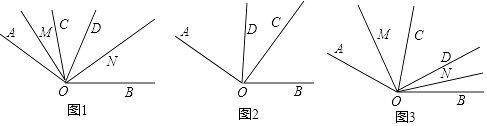
(1)若∠COD=180°﹣α時,探索下面兩個問題: ①如圖1,當OC在OD左側,求∠MON的度數;
②當OC在OD右側,請在圖2內補全圖形,并求出∠MON的度數(用含α的代數式表示);
(2)如圖3,當∠COD=kα,且OC在OD左側時,直接寫出∠MON的度數(用含α、k的代數式表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,點O為直線AB上一點,過點O作射線OC,使∠BOC=120°,將一直角三角板的直角頂點放在點O處,一邊OM在射線OB上,另一邊ON在直線AB的下方. 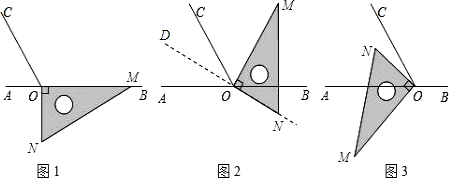
(1)將圖1中的三角板繞點O逆時針旋轉至圖2,使一邊OM在∠BOC的內部,且恰好平分∠BOC,設ON的反向延長線為OD,則∠COD=°,∠AOD=°.
(2)將圖1中的三角板繞點O順時針旋轉至圖3,使ON在∠AOC的內部,求∠AOM﹣∠NOC的度數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com