
【題目】如圖,在△ABC中,已知∠ABC=30°,點D在BC上,點E在AC上,∠BAD=∠EBC,AD交BE于F.
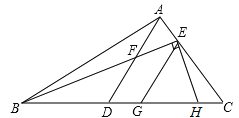
(1)求∠BFD的度數;
(2)若EG∥AD交BC于G,EH⊥BE交BC于H,求∠HEG的度數.
【答案】(1)30°;(2)60°.
【解析】
試題分析:(1)先根據∠ABC=30°,∠BAD=∠EBC可知,∠BAD+∠ABF=∠EBC+∠ABF=∠ABC=30°,再根據三角形外角的性質即可得出結論;
(2)先根據EG∥AD,∠BFD=30°可知∠BEG=30°,再根據EH⊥BE可知∠BEH=90°,故可求出∠HEG的度數.
試題解析:(1)∵∠ABC=30°,∠BAD=∠EBC,
∴∠BAD+∠ABF=∠EBC+∠ABF=∠ABC=30°,
∵∠BFD是△ABF的外角,
∴∠BFD=∠BAD+∠ABF=30°;
(2)∵EG∥AD,∠BFD=30°,
∴∠BEG=∠BFD=30°,
∵EH⊥BE,
∴∠BEH=90°,
∴∠HEG=∠BEH-∠BDG=90°-30°=60°.


科目:初中數學 來源: 題型:
【題目】如圖,小李制作了一張△ABC紙片,點D、E分別在邊AB、AC上,現將△ABC沿著DE折疊壓平,使點A落在點A′位置.若∠A=75°,則∠1+∠2= .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,正方形OABC的邊長為4,頂點A、C分別在x軸、y軸的正半軸,拋物線y=﹣![]() x2+bx+c經過B、C兩點,點D為拋物線的頂點,連接AC、BD、CD.
x2+bx+c經過B、C兩點,點D為拋物線的頂點,連接AC、BD、CD.
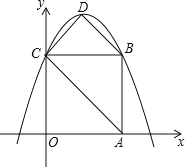
(1)求此拋物線的解析式.
(2)求此拋物線頂點D的坐標和四邊形ABCD的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在外來文化的滲透和商家的炒作下,過洋節儼然成為現今青少年一種時尚,圣誕節前期,三位同學到某超市調研一種進價為每個2元的蘋果的銷售情況,請根據小麗提供的信息,解答小華和小明提出的問題.
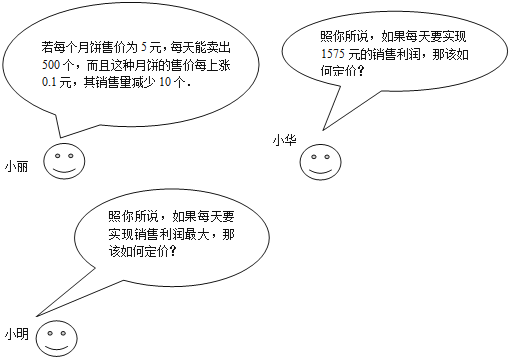
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義兩種新變換:①f(a,b)=(a,-b),如f(1,2)=(1,-2);②g(a,b)=(b,a),如g(1,2)=(2,1).據此得g(f(5,-6))=_________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】∠1與∠2是兩條直線被第三條直線所截的同位角,若∠1=50°,則∠2為( )
A. 50° B. 130° C. 50°或130° D. 不能確定
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com