
【題目】![]() 問題發現
問題發現
如圖![]() 和
和![]() 均為等邊三角形,點
均為等邊三角形,點![]() 在同一直線上,連接BE.
在同一直線上,連接BE.
填空:
![]() 的度數為______;
的度數為______;
![]() 線段
線段![]() 之間的數量關系為______.
之間的數量關系為______.
![]() 拓展探究
拓展探究
如圖![]() 和
和![]() 均為等腰直角三角形,
均為等腰直角三角形,![]() ,點
,點![]() 在同一直線上,CM為
在同一直線上,CM為![]() 中DE邊上的高,連接BE,請判斷
中DE邊上的高,連接BE,請判斷![]() 的度數及線段
的度數及線段![]() 之間的數量關系,并說明理由.
之間的數量關系,并說明理由.
![]() 解決問題
解決問題
如圖3,在正方形ABCD中,![]() ,若點P滿足
,若點P滿足![]() ,且
,且![]() ,請直接寫出點A到BP的距離.
,請直接寫出點A到BP的距離.
【答案】![]() ;
;![]() ;
;![]() ,理由見解析;
,理由見解析; ![]() 點A到BP的距離為
點A到BP的距離為![]() 或
或![]() .
.
【解析】分析:(1)由條件易證△ACD≌△BCE,從而得到:AD=BE,∠ADC=∠BEC.由點A,D,E在同一直線上可求出∠ADC,從而可以求出∠AEB的度數.
(2)仿照(1)中的解法可求出∠AEB的度數,證出AD=BE;由△DCE為等腰直角三角形及CM為△DCE中DE邊上的高可得CM=DM=ME,從而證到AE=2CH+BE.
(3)由PD=1可得:點P在以點D為圓心,1為半徑的圓上;由∠BPD=90°可得:點P在以BD為直徑的圓上.顯然,點P是這兩個圓的交點,由于兩圓有兩個交點,接下來需對兩個位置分別進行討論.然后,添加適當的輔助線,借助于(2)中的結論即可解決問題.
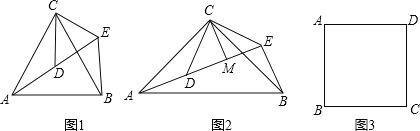
詳解:(1)①如圖1.∵△ACB和△DCE均為等邊三角形,∴CA=CB,CD=CE,∠ACB=∠DCE=60°,∴∠ACD=∠BCE.
在△ACD和△BCE中,∵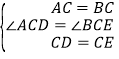 ,
,
∴△ACD≌△BCE(SAS),∴∠ADC=∠BEC.
∵△DCE為等邊三角形,∴∠CDE=∠CED=60°.
∵點A,D,E在同一直線上,∴∠ADC=120°,∴∠BEC=120°,∴∠AEB=∠BEC﹣∠CED=60°.
故答案為:60°.
②∵△ACD≌△BCE,∴AD=BE.
故答案為:AD=BE.
(2)∠AEB=90°,AE=BE+2CM.
理由:如圖2.∵△ACB和△DCE均為等腰直角三角形,∴CA=CB,CD=CE,∠ACB=∠DCE=90°,∴∠ACD=∠BCE.
在△ACD和△BCE中,∵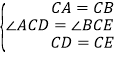 ,
,
∴△ACD≌△BCE(SAS),∴AD=BE,∠ADC=∠BEC.
∵△DCE為等腰直角三角形,∴∠CDE=∠CED=45°.
∵點A,D,E在同一直線上,∴∠ADC=135°,∴∠BEC=135°,∴∠AEB=∠BEC﹣∠CED=90°.
∵CD=CE,CM⊥DE,
∵∠DCE=90°,∴DM=ME=CM,∴AE=AD+DE=BE+2CM.
(3)點A到BP的距離為![]() 或
或![]() .
.
理由如下:
∵PD=1,∴點P在以點D為圓心,1為半徑的圓上.
∵∠BPD=90°,∴點P在以BD為直徑的圓上,∴點P是這兩圓的交點.
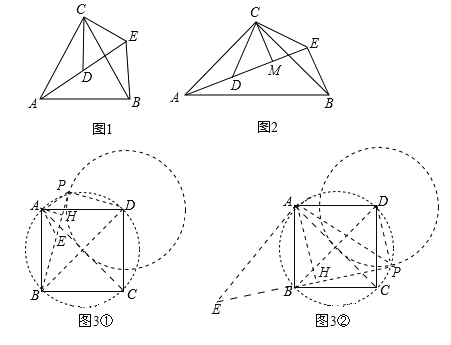
①當點P在如圖3①所示位置時,連接PD、PB、PA,作AH⊥BP,垂足為H,過點A作AE⊥AP,交BP于點E,如圖3①.
∵四邊形ABCD是正方形,∴∠ADB=45°.AB=AD=DC=BC=![]() ,∠BAD=90°,∴BD=2.
,∠BAD=90°,∴BD=2.
∵DP=1,∴BP=![]() .
.
∵∠BPD=∠BAD=90°,∴A、P、D、B在以BD為直徑的圓上,∴∠APB=∠ADB=45°,∴△PAE是等腰直角三角形.
又∵△BAD是等腰直角三角形,點B、E、P共線,AH⊥BP,∴由(2)中的結論可得:BP=2AH+PD,∴![]() =2AH+1,∴AH=
=2AH+1,∴AH=![]() .
.
②當點P在如圖3②所示位置時,連接PD、PB、PA,作AH⊥BP,垂足為H,過點A作AE⊥AP,交PB的延長線于點E,如圖3②.
同理可得:BP=2AH﹣PD,∴![]() =2AH﹣1,∴AH=
=2AH﹣1,∴AH=![]() .
.
綜上所述:點A到BP的距離為![]() 或
或![]() .
.


 口算小狀元口算速算天天練系列答案
口算小狀元口算速算天天練系列答案 天天練口算系列答案
天天練口算系列答案科目:初中數學 來源: 題型:
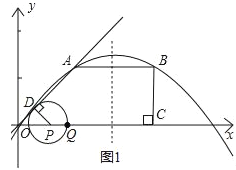
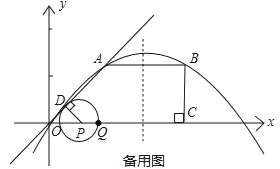
【題目】如圖,O是平面直角坐標系的原點.在四邊形OABC中,AB∥OC,BC⊥x軸于C,A(1,1),B(3,1),動點P從O點出發,沿x軸正方向以2個單位/秒的速度運動.設P點運動的時間為t秒(0<t<2).
(1)求經過O、A、B三點的拋物線的解析式;
(2)過P作PD⊥OA于D,以點P為圓心,PD為半徑作⊙P,⊙P在點P的右側與x軸交于點Q.
①則P點的坐標為_____,Q點的坐標為_____;(用含t的代數式表示)
②試求t為何值時,⊙P與四邊形OABC的兩邊同時相切;
③設△OPD與四邊形OABC重疊的面積為S,請直接寫出S與t的函數解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,在正方形ABCD中,![]() ,點E,F分別在BC、CD上,
,點E,F分別在BC、CD上,![]() ,試探究
,試探究![]() 面積的最小值。
面積的最小值。
下面是小麗的探究過程:
(1)延長EB至G,使![]() ,連接AG,可以證明
,連接AG,可以證明![]() .請完成她的證明;
.請完成她的證明;
(2)設![]() ,
,![]() ,
,![]()
①結合(1)中結論,通過計算得到![]() 與x的部分對應值。請求出表格中a的值:(寫出解答過程)
與x的部分對應值。請求出表格中a的值:(寫出解答過程)
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 10 | 8.18 | 6.67 | 5.38 | 4.29 | 3.33 | a | 1.76 | 1.11 | 0.53 | 0 |
②利用上表和(1)中的結論通過描點、連線可以分別畫出函數![]() 、
、![]() 的圖像、請在圖②中完善她的畫圖;
的圖像、請在圖②中完善她的畫圖;
③根據以上探究,估計![]() 面積的最小值約為(結果估計到0.1)。
面積的最小值約為(結果估計到0.1)。
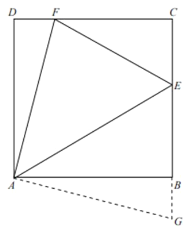
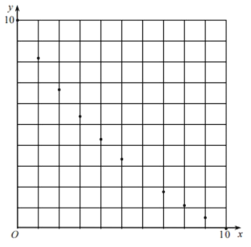
圖① 圖②
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在今年我市初中學業水平考試體育學科的女子800米耐力測試中,某考點同時起跑的小瑩和小梅所跑的路程S(米)與所用時間t(秒)之間的函數圖象分別為線段OA和折線OBCD,下列說法正確的是( )

A、小瑩的速度隨時間的增大而增大B、小梅的平均速度比小瑩的平均速度大
C、在起跑后180秒時,兩人相遇D、在起跑后50秒時,小梅在小瑩的前面
查看答案和解析>>
科目:初中數學 來源: 題型:
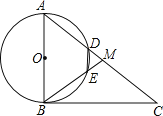
【題目】如圖,在![]() 中,
中,![]() ,點M是AC的中點,以AB為直徑作
,點M是AC的中點,以AB為直徑作![]() 分別交
分別交![]() 于點
于點![]() .
.
![]() 求證:
求證:![]() ;
;
![]() 填空:
填空:
![]() 若
若![]() ,當
,當![]() 時,
時,![]() ______;
______;
![]() 連接
連接![]() ,當
,當![]() 的度數為______時,四邊形ODME是菱形.
的度數為______時,四邊形ODME是菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】溫度通常有兩種表示方法:華氏度(單位:℉)與攝氏度(單位:℃),已知華氏度數![]() 與攝氏度數
與攝氏度數![]() 之間是一次函數關系,下表列出了部分華氏度與攝氏度之間的對應關系:
之間是一次函數關系,下表列出了部分華氏度與攝氏度之間的對應關系:
攝氏度數 | … | 0 | … | 35 | … | 100 | … |
華氏度數 | … | 32 | … | 95 | … | 212 | … |
(1)選用表格中給出的數據,求y關于x的函數解析式;
(2)有一種溫度計上有兩個刻度,即測量某一溫度時左邊是攝氏度,右邊是華氏度,那么在多少攝氏度時,溫度計上右邊華氏度的刻度正好比左邊攝氏度的刻度大56?
查看答案和解析>>
科目:初中數學 來源: 題型:
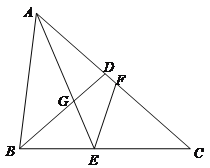
【題目】如圖,已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,D是AC邊上一點,且
,D是AC邊上一點,且![]() ,聯結BD,點E、F分別是BC、AC上兩點(點E不與B、C重合),
,聯結BD,點E、F分別是BC、AC上兩點(點E不與B、C重合),![]() ,AE與BD相交于點G.
,AE與BD相交于點G.
(1)求證:BD平分![]() ;
;
(2)設![]() ,
,![]() ,求
,求![]() 與
與![]() 之間的函數關系式;
之間的函數關系式;
(3)聯結FG,當![]() 是等腰三角形時,求BE的長度.
是等腰三角形時,求BE的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
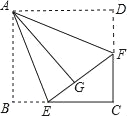
【題目】如圖,在四邊形紙片ABCD中,∠B=∠D=90°,點E,F分別在邊BC,CD上,將AB,AD分別沿AE,AF折疊,點B,D恰好都和點G重合,∠EAF=45°.
(1)求證:四邊形ABCD是正方形;
(2)求證:三角形ECF的周長是四邊形ABCD周長的一半;
(3)若EC=FC=1,求AB的長度.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com