
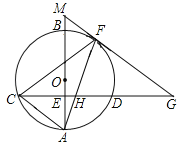
【題目】如圖,AB是⊙O的直徑,CD⊥AB,交⊙O于C、D兩點,交AB點E、F是弧BD上一點,過點F作一條直線,交CD的延長線于點G,交AB的延長線于點M.連結AF,交CD于點H,GF=GH.
(1)求證:MG是⊙O的切線;
(2)若弧AF=弧CF,求證:HC=AC;
(3)在(2)的條件下,若tanG=![]() ,AE=6,求GM的值.
,AE=6,求GM的值.
【答案】(1)證明見解析;(2)證明見解析;(3)GM=![]() .
.
【解析】
(1)連接OF,先證明∠GFH=∠GHF=∠AHE,再證明OF⊥GM即可.
(2)證明AC∥GM,再證明∠CAH=∠CHA即可得到答案.
(3)解直角三角形求出EC,AC,設GF=GH=x,則CG=CH+GH=AC+GH=10+x,利用切線長定理構建方程求出x即可解決問題.
(1)證明:連接OF.
∴AB⊥CD,
∴∠AEH=90°,
∴∠EAH+∠AHE=90°,
∵GF=GH,
∴∠GFH=∠GHF=∠AHE,
∵OA=OF,
∴∠OAF=∠OFA,
∴∠OFA+∠GFH=90°,
∴OF⊥GM,
∴MG是⊙O的切線.
(2)證明:∵弧AF=弧CF,
∴OF垂直平分線段AC
∵OF⊥MG,
∴AC∥GM,
∴∠CAH=∠GFH,
∵∠CHA=∠GHF,∠HGF=∠GFH,
∴∠CAH=∠CHA,
∴CA=CH.
(3)解:∵AC∥GM,
∴∠G=∠ACH,
∴tan∠CAH=tan∠G=![]() ,
,
∵AE=6,
∴EC=8,AC=![]() ,
,
設GF=GH=x,則CG=CH+GH=AC+GH=10+x,
∵CD=2EC=16,
∴GD=10+x﹣16=x﹣6,
∵GF2=GDGC,
∴x2=(x﹣6)(x+10),
解得x=15,
∴EG=CG﹣CE=25﹣8=17,
∵tan∠G=![]() ,
,
∴EM=![]() ,
,
∴GM=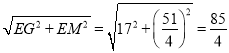 .
.


科目:初中數學 來源: 題型:
【題目】定義:如果一個點的縱坐標是橫坐標的二倍,則稱該點為“倍點”
(1)若點![]() 是雙曲線
是雙曲線![]() 上的倍點,則
上的倍點,則![]() ;
;
(2)求出直線![]() 上的倍點的坐標;
上的倍點的坐標;
(3)若拋物線![]() 上有且只有一個倍點,求
上有且只有一個倍點,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1.在![]() 中,
中,![]() 把
把![]() 沿對角線
沿對角線![]() 所在的直線折疊,使點
所在的直線折疊,使點![]() 落在點
落在點![]() 處,
處,![]() 交
交![]() 于點
于點![]() .連接
.連接![]() .
.

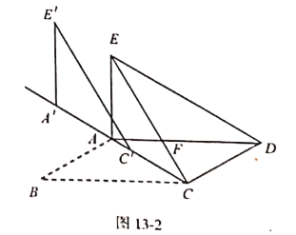
(1)求證:![]() ;
;
(2)求證:![]() 為等腰三角形;
為等腰三角形;
(3)將圖1中![]() 的沿射線
的沿射線![]() 方向平移得到
方向平移得到![]() (如圖2所示) .若在
(如圖2所示) .若在![]() 中,
中,![]() . 當
. 當![]() 時,直接寫出
時,直接寫出![]() 平移的距離.
平移的距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
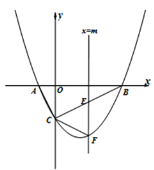
【題目】如圖,拋物線![]() 與x軸交于A、B兩點,與y軸交于點C,已知A(–1,0),且直線BC的解析式為y=
與x軸交于A、B兩點,與y軸交于點C,已知A(–1,0),且直線BC的解析式為y=![]() x-2,作垂直于x軸的直線
x-2,作垂直于x軸的直線![]() ,與拋物線交于點F,與線段BC交于點E(不與點B和點C重合).
,與拋物線交于點F,與線段BC交于點E(不與點B和點C重合).
(1)求拋物線的解析式;
(2)若△CEF是以CE為腰的等腰三角形,求m的值;
(3)點P為y軸左側拋物線上的一點,過點P作![]() 交直線BC于點M,連接PB,若以P、M、B為頂點的三角形與△ABC相似,求P點的坐標.
交直線BC于點M,連接PB,若以P、M、B為頂點的三角形與△ABC相似,求P點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,AB=3,BC=4,動點P從A點出發,按A→B→C的方向在AB和BC上移動,記PA=x,點D到直線PA的距離為y,則y關于x的函數圖象大致是( )

A. B.
B.
C. D.
D.
查看答案和解析>>
科目:初中數學 來源: 題型:
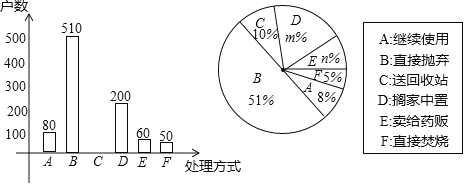
【題目】家庭過期藥品屬于“國家危險廢物”,處理不當將污染環境,危害健康.某市藥監部門為了解市民家庭處理過期藥品的方式,決定對全市家庭作一次簡單隨機抽樣調査.
(1)下列選取樣本的方法最合理的一種是 .(只需填上正確答案的序號)
①在市中心某個居民區以家庭為單位隨機抽取;②在全市醫務工作者中以家庭為單位隨機抽取;③在全市常住人口中以家庭為單位隨機抽取.
(2)本次抽樣調査發現,接受調査的家庭都有過期藥品,現將有關數據呈現如圖:
①m= ,n= ;
②補全條形統計圖;
③扇形統計圖中扇形C的圓心角度數是 ;
④家庭過期藥品的正確處理方式是送回收點,若該市有180萬戶家庭,請估計大約有多少戶家庭處理過期藥品的方式是送回收點.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知四個命題:①如果一個數的相反數等于它本身,則這個數是0;②一個數的倒數等于它本身,則這個數是1;③一個數的算術平方根等于它本身,則這個數是1或0;④甲、乙兩射擊運動員分別射擊10次,他們射擊成績的方差分別為![]() =5,
=5,![]() =2,這一過程中乙發揮比甲更穩定.⑤點M(a,b),N(c,d)都在反比例函數y=
=2,這一過程中乙發揮比甲更穩定.⑤點M(a,b),N(c,d)都在反比例函數y=![]() 的圖象上.若a<c,則b>d.其中真命題有( )個.
的圖象上.若a<c,則b>d.其中真命題有( )個.
A.2B.3C.4D.5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某小區有甲、乙兩座樓房,樓間距BC為50米,在乙樓頂部A點測得甲樓頂部D點的仰角為37°,在乙樓底部B點測得甲樓頂部D點的仰角為60°,則甲、乙兩樓的高度分別為多少?(結果精確到1米,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,D是AB邊上一點,⊙O過D、B、C三點,∠DOC=2∠ACD=90°.

(1)求證:直線AC是⊙O的切線;
(2)如果∠ACB=75°,⊙O的半徑為2,求BD的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com