
【題目】如圖所示,![]() 是
是![]() 的直徑,
的直徑,![]() 與
與![]() 相切于點(diǎn)
相切于點(diǎn)![]() ,與
,與![]() 的延長(zhǎng)線交于點(diǎn)
的延長(zhǎng)線交于點(diǎn)![]() .
.
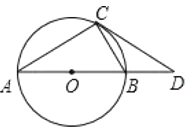
(1)求證:![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() 的半徑.
的半徑.
【答案】(1)見解析 (2)![]()
【解析】
(1) 首先連接CO,根據(jù)CD與⊙O相切于點(diǎn)C,可得:∠OCD=90;然后根據(jù)AB是⊙O的直徑得:∠ACB=90°,據(jù)此判斷出∠ACD=∠BCD=∠A,即可推得△ADC∽△CDB.
(2)首先設(shè)CD為4t,則AB=![]() ·4t=6t,OC=OB=
·4t=6t,OC=OB=![]() ·4t=3t,用t表示出OD、BD;然后根據(jù)△ADC∽△CDB,可得:
·4t=3t,用t表示出OD、BD;然后根據(jù)△ADC∽△CDB,可得:![]() ,據(jù)此求出CB的值,即可求出⊙O半徑.
,據(jù)此求出CB的值,即可求出⊙O半徑.
(1)證明:連接OC,
∵CD是⊙O的切線,∴∠OCD=90 o
又∵AB是⊙O的直徑,∴∠ACB=90o
∴∠1=∠2
又OA=OC,∴∠1=∠A=∠2
∵ ∠D=∠D,
∴ △ADC∽△CDB
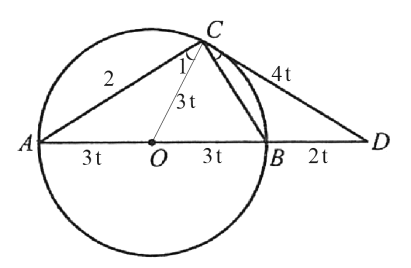
(2)解:設(shè)CD=4t,則AB=![]() CD=6t,∴OA=OB=3t
CD=6t,∴OA=OB=3t
在Rt△OCD中,OC=OA=OB=3t,CD=4t
∴![]() ,∴
,∴![]()
由(1)知△ADC∽△CDB,∴![]() ,∴CB=1
,∴CB=1
∴![]() ,
,
∴⊙O的半徑為![]()



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
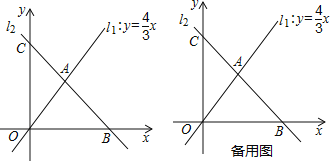
【題目】如圖,直線![]() 與直線
與直線![]() 交于點(diǎn)
交于點(diǎn)![]() ,直線
,直線![]() 與
與![]() 軸、
軸、![]() 軸分別交于點(diǎn)
軸分別交于點(diǎn)![]() 、點(diǎn)
、點(diǎn)![]() .
.
(1)求直線![]() 的關(guān)系式;
的關(guān)系式;
(2)若與![]() 軸平行的直線
軸平行的直線![]() 與直線
與直線![]() 分別交于點(diǎn)
分別交于點(diǎn)![]() 、點(diǎn)
、點(diǎn)![]() ,則
,則![]() 的面積為_____(直接填空);
的面積為_____(直接填空);
(3)在(2)的情況下,把![]() 沿著過原點(diǎn)的直線
沿著過原點(diǎn)的直線![]() 翻折,當(dāng)點(diǎn)
翻折,當(dāng)點(diǎn)![]() 落在直線
落在直線![]() 上時(shí),直接寫出
上時(shí),直接寫出![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
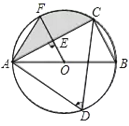
【題目】如圖,已知AB是⊙O的直徑,點(diǎn)C、D在⊙O上,∠D=60°,且AB=6,過O點(diǎn)作OE⊥AC,垂足為E.
(1)求OE的長(zhǎng);
(2)若OE的延長(zhǎng)線交⊙O于點(diǎn)F,求弦AF、AC和弧CF圍成的圖形(陰影部分)的面積.(結(jié)果精確到0.01)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
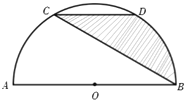
【題目】如圖,![]() 是半圓
是半圓![]() 的直徑,點(diǎn)
的直徑,點(diǎn)![]() 、
、![]() 是半圓
是半圓![]() 的三等分點(diǎn),弦
的三等分點(diǎn),弦![]() .現(xiàn)將一飛鏢擲向該圖,則飛鏢落在陰影區(qū)域的概率為( )
.現(xiàn)將一飛鏢擲向該圖,則飛鏢落在陰影區(qū)域的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
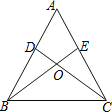
【題目】如圖,點(diǎn)D、E分別為△ABC的邊AB、AC上的點(diǎn),BE與CD相交于點(diǎn)O,現(xiàn)有四個(gè)條件:①AB=AC;②OB=OC;③∠ABE=∠ACD;④BE=CD,選擇其中2個(gè)條件作為題設(shè),余下2個(gè)條件作為結(jié)論,所有命題中,真命題的個(gè)數(shù)為( )
A. .3B. .4C. .5D. 、6
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖所示的拋物線對(duì)稱軸是直線x=1,與x軸有兩個(gè)交點(diǎn),與y軸交點(diǎn)坐標(biāo)是(0,3),把它向下平移2個(gè)單位后,得到新的拋物線解析式是 y=ax2+bx+c,以下四個(gè)結(jié)論:①b2﹣4ac<0,②abc<0,③4a+2b+c=1,④a﹣b+c>0中,判斷正確的有( )
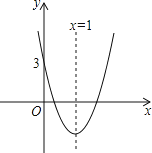
A. ②③④B. ①②③C. ②③D. ①④
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
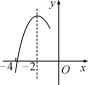
【題目】如圖,拋物線y=ax2+bx+c(a≠0)的對(duì)稱軸為直線x=-2,與x軸的一個(gè)交點(diǎn)在(-3,0)和(-4,0)之間,其部分圖象如圖所示.則下列結(jié)論:①4a-b=0;②c<0;③-3a+c>0;④4a-2b>at2+bt(t為實(shí)數(shù));⑤點(diǎn)![]() ,
,![]() ,
,![]() 是該拋物線上的點(diǎn),則y1<y2<y3.其中正確結(jié)論的個(gè)數(shù)是( )
是該拋物線上的點(diǎn),則y1<y2<y3.其中正確結(jié)論的個(gè)數(shù)是( )
A.4B.3C.2D.1
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
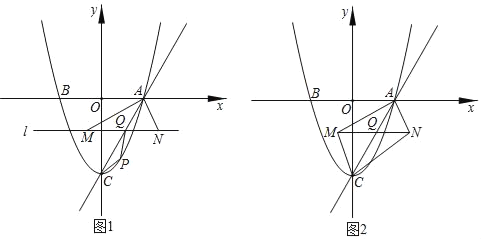
【題目】如圖1,拋物線y=x2﹣3與x軸交于AB兩點(diǎn)(點(diǎn)A在點(diǎn)B的右側(cè)),與y軸交于點(diǎn)C,連接AC.點(diǎn)Q是線段AC上的動(dòng)點(diǎn),過Q作直線l∥x軸,直線1與∠BAC的平分線交于點(diǎn)M,與∠CAx的平分線交于點(diǎn)N.
(1)P是直線AC下方拋物線上一動(dòng)點(diǎn),連接PA,PC,當(dāng)△PAC的面積最大時(shí),求PQ+![]() AM的最小值;
AM的最小值;
(2)如圖2,連接MC,NC,當(dāng)四邊形AMCN為矩形時(shí),將△AMN沿著直線AC平移得到△A'M'N',邊A'M'所在的直線與y軸交于D點(diǎn),若△DM'N'為等腰三角形時(shí),求OD的長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,拋物線![]() 與
與![]() 軸交于
軸交于![]() 、
、![]() 兩點(diǎn)(點(diǎn)
兩點(diǎn)(點(diǎn)![]() 在點(diǎn)
在點(diǎn)![]() 的左側(cè)),點(diǎn)
的左側(cè)),點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,與
,與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,作直線
,作直線![]() .動(dòng)點(diǎn)
.動(dòng)點(diǎn)![]() 在
在![]() 軸上運(yùn)動(dòng),過點(diǎn)
軸上運(yùn)動(dòng),過點(diǎn)![]() 作
作![]() 軸,交拋物線于點(diǎn)
軸,交拋物線于點(diǎn)![]() ,交直線
,交直線![]() 于點(diǎn)
于點(diǎn)![]() ,設(shè)點(diǎn)
,設(shè)點(diǎn)![]() 的橫坐標(biāo)為
的橫坐標(biāo)為![]() .
.
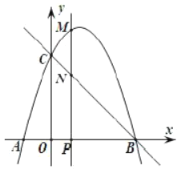
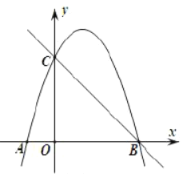
(1)直接寫出拋物線的解析式__________和直線![]() 的解析式_________;
的解析式_________;
(2)當(dāng)點(diǎn)![]() 在線段
在線段![]() 上運(yùn)動(dòng)時(shí),直接寫出線段
上運(yùn)動(dòng)時(shí),直接寫出線段![]() 長(zhǎng)度的最大值_________;
長(zhǎng)度的最大值_________;
(3)當(dāng)點(diǎn)![]() 在線段
在線段![]() 上運(yùn)動(dòng)時(shí),若
上運(yùn)動(dòng)時(shí),若![]() 是以
是以![]() 為腰的等腰直角三角形時(shí),求
為腰的等腰直角三角形時(shí),求![]() 的值;
的值;
(4)當(dāng)以![]() 、
、![]() 、
、![]() 、
、![]() 為頂點(diǎn)的四邊形是平行四邊形時(shí),求出
為頂點(diǎn)的四邊形是平行四邊形時(shí),求出![]() 的值.
的值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com