
【題目】定義:若拋物線![]() 與拋物線
與拋物線![]() 的開口大小相同,方向相反,且拋物線
的開口大小相同,方向相反,且拋物線![]() 經過
經過![]() 的頂點,我們稱拋物線
的頂點,我們稱拋物線![]() 為
為![]() 的“友好拋物線”.
的“友好拋物線”.
(1)若![]() 的表達式為
的表達式為![]() ,求
,求![]() 的“友好拋物線”的表達式;
的“友好拋物線”的表達式;
(2)已知拋物線![]() 為
為![]() 的“友好拋物線”.求證:拋物線
的“友好拋物線”.求證:拋物線![]() 也是
也是![]() 的“友好拋物線”;
的“友好拋物線”;
(3)平面上有點![]() ,
,![]() ,拋物線
,拋物線![]() 為
為![]() 的“友好拋物線”,且拋物線
的“友好拋物線”,且拋物線![]() 的頂點在第一象限,縱坐標為2,當拋物線
的頂點在第一象限,縱坐標為2,當拋物線![]() 與線段
與線段![]() 沒有公共點時,求
沒有公共點時,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() 的“友好拋物線”為:
的“友好拋物線”為:![]() ;(2)見解析;(3)
;(2)見解析;(3)![]() 或
或![]() .
.
【解析】
(1)設![]() 的“友好拋物線”的表達式為:
的“友好拋物線”的表達式為:![]() ,根據
,根據![]() 可得其頂點坐標,代入
可得其頂點坐標,代入![]() 可得
可得![]() 的值,進而得出
的值,進而得出![]() 的“友好拋物線”;
的“友好拋物線”;
(2)先求出拋物線![]() 和
和![]() 的頂點坐標,根據
的頂點坐標,根據![]() 過
過![]() 的頂點,得出
的頂點,得出![]() ,進而得到拋物線
,進而得到拋物線![]() 經過
經過![]() 的頂點,再根據
的頂點,再根據![]() 與
與![]() 的開口大小相同,方向相反,即可得出拋物線
的開口大小相同,方向相反,即可得出拋物線![]() 也是
也是![]() 的“友好拋物線”;
的“友好拋物線”;
(3)根據“友好拋物線”的定義,得到![]() ,進而得到
,進而得到![]() 的頂點為
的頂點為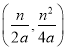 .
.
根據拋物線![]() 的頂點在第一象限,縱坐標為2,可得
的頂點在第一象限,縱坐標為2,可得![]() .
.
再根據![]() 經過點
經過點![]() ,得到
,得到![]() .根據
.根據![]() 經過點
經過點![]() ,得到
,得到![]() .
.
進而得出拋物線![]() 與線段
與線段![]() 沒有公共點時,
沒有公共點時,![]() 的取值范圍.
的取值范圍.
解:(1)依題意,可設![]() 的“友好拋物線”的表達式為:
的“友好拋物線”的表達式為:![]() ,
,
∵![]() ,
,
∴![]() 的頂點為
的頂點為![]() .
.
∵![]() 過點
過點![]() ,
,
∴![]() ,即
,即![]() .
.
∴![]() 的“友好拋物線”為:
的“友好拋物線”為:![]() .
.
(2)![]() 的頂點為
的頂點為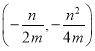 ,
,
![]() 的頂點為
的頂點為![]() ,
,
∵![]() 為
為![]() 的“友好拋物線”,
的“友好拋物線”,
∴![]() .
.
∵![]() 過
過![]() 的頂點,
的頂點,
∴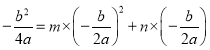 .
.
化簡得:![]() .
.
把![]() 代入
代入![]() ,得
,得
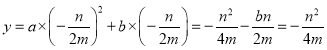 .
.
∴拋物線![]() 經過
經過![]() 的頂點.
的頂點.
又∵![]() 與
與![]() 的開口大小相同,方向相反,
的開口大小相同,方向相反,
∴拋物線![]() 也是
也是![]() 的“友好拋物線”.
的“友好拋物線”.
(3)∵拋物線![]() 為
為![]() 的“友好拋物線”,
的“友好拋物線”,
∴![]() .
.
∴![]() 的頂點為
的頂點為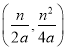 .
.
∵拋物線![]() 的頂點在第一象限,縱坐標為2,
的頂點在第一象限,縱坐標為2,
∴![]() ,即
,即![]() .
.
當![]() 經過點
經過點![]() 時,
時,![]() ,
,
∴![]() .
.
當![]() 經過點
經過點![]() 時,
時,![]() ,
,
∴![]() .
.
由此可知:![]() 時,拋物線
時,拋物線![]() 與線段
與線段![]() 有公共點,
有公共點,
∴拋物線![]() 與線段
與線段![]() 沒有公共點時,
沒有公共點時,![]() 或
或![]() .
.


 全能測控期末小狀元系列答案
全能測控期末小狀元系列答案科目:初中數學 來源: 題型:
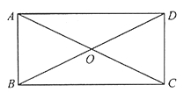
【題目】如圖,四邊形ABCD中,對角線AC、BD相交于點O,AO=OC,BO=OD,且∠AOB=2∠OAD.
(1)求證:四邊形ABCD是矩形;
(2)若∠AOB∶∠ODC=4∶3,求∠ADO的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在⊙O中,半徑OA⊥弦BC于點H,點D在優弧BC上
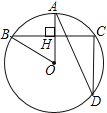
(1)若∠AOB=50°,求∠ADC的度數;
(2)若BC=8,AH=2,求⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 為等邊三角形,
為等邊三角形,![]() ,連接
,連接![]() ,
,![]() 為
為![]() 中點.
中點.
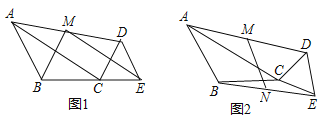
(1)如圖1,當![]() ,
,![]() ,
,![]() 三點共線時,請畫出
三點共線時,請畫出![]() 關于點
關于點![]() 的中心對稱圖形,判斷
的中心對稱圖形,判斷![]() 與
與![]() 的位置關系是 ;
的位置關系是 ;
(2)如圖2,當A,![]() ,
,![]() 三點共線時,問(1)中結論是否成立,若成立,給出證明,若不成立,請說明理由;
三點共線時,問(1)中結論是否成立,若成立,給出證明,若不成立,請說明理由;
(3)如圖2,取![]() 中點
中點![]() ,連
,連![]() ,將
,將![]() 繞點
繞點![]() 旋轉,直接寫出旋轉過程中線段
旋轉,直接寫出旋轉過程中線段![]() 的取值范圍是 .
的取值范圍是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于![]() 的方程
的方程![]() .
.
(1)求證:無論![]() 取何值,這個方程總有實數根.
取何值,這個方程總有實數根.
(2)若方程的兩根都是正數,求![]() 的取值范圍.
的取值范圍.
(3)以方程的兩根為![]() 兩邊,斜邊為
兩邊,斜邊為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
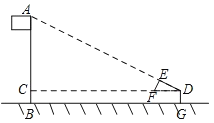
【題目】如圖,某校數學興趣小組利用自制的直角三角形硬紙板DEF來測量操場旗桿AB的高度,他們通過調整測量位置,使斜邊DF與地面保持平行,并使邊DE與旗桿頂點A在同一直線上,已知DE=0.5m,EF=0.25m,目測點D到地面的距離DG=1.5m,到旗桿的水平距離DC=20m,則旗桿的高度為( )
A.![]() mB.
mB.![]() m
m
C.11.5mD.10m
查看答案和解析>>
科目:初中數學 來源: 題型:
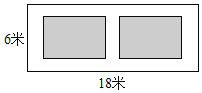
【題目】如圖,某小區有一長為18米,寬為6米的矩形空地,計劃在其中修建兩塊相同的矩形綠地,它們面積之和為60平方米,兩塊綠地之間及周邊留有寬度相等的人行通道,則人行道的寬度為( )米.
A. 2B. 1C. 8或1D. 8
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com