
【題目】4月12日華為新出的型號為“P30 Pro”的手機在上海召開發布會,某華為手機專賣網店抓住商機,購進10000臺“P30 Pro”手機進行銷售,每臺的成本是4400元,在線同時向國內、國外發售.第一個星期,國內銷售每臺售價是5400元,共獲利100萬元,國外銷售也售出相同數量該款手機,但每臺成本增加400元,獲得的利潤卻是國內的6倍.
(1)求該店銷售該款華為手機第一個星期在國外的售價是多少元?
(2)受中美貿易戰影響,第二個星期,國內銷售每臺該款手機售價在第一個星期的基礎上降低m%,銷量上漲5m%;國外銷售每臺售價在第一個星期的基礎上上漲m%,并且在第二個星期將剩下的手機全部賣完,結果第二個星期國外的銷售總額比國內的銷售總額多6993萬元,求m的值.
【答案】(1)10800元;(2)m=10.
【解析】
(1)根據(國外的售價-成本)×銷售的數量=國內的6倍,列方程解出即可;
(2)根據第二個星期國外的銷售總額-國內的銷售總額=6993萬元,利用換元法解方程可解答.
解:(1)設該店銷售該款華為手機第一個星期在國外的售價是x元,
根據題意得:![]() [x-(4400+400)]=6×100,x=10800,
[x-(4400+400)]=6×100,x=10800,
答:該店銷售該款華為手機第一個星期在國外的售價是10800元;
(2)第一個星期國內銷售手機的數量為:![]() =1000(臺),
=1000(臺),
由題意得:10800(1+m%)×[10000-2000-1000(1+5m%)]-5400(1-m%)×1000(1+5m%)=69930000,
10800(1+m%)(7000-5000m%)-5400×1000(1-m%)(1+5m%)=69930000,
1080(1+m%)(7-5m%)-540(1-m%)(1+5m%)=6993,
設m%=a,則原方程化為:1080(1+a)(7-5a)-540(1-a)(1+5a)=6993,
360(1+a)(7-5a)-180(1-a)(1+5a)=2331,
a2=0.01,
a=0.1或-0.1(舍),
∴m=10.


科目:初中數學 來源: 題型:
【題目】為了比較市場上甲、乙兩種電子鐘每日走時誤差的情況,從這兩種電子鐘中,各隨機抽取10臺進行測試,兩種電子鐘走時誤差的數據如下表(單位:秒):
編號 類型 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 九 | 十 |
甲種電子鐘 | 1 | -3 | -4 | 4 | 2 | -2 | 2 | -1 | -1 | 2 |
乙種電子鐘 | 4 | -3 | -1 | 2 | -2 | 1 | -2 | 2 | -2 | 1 |
(1) 計算甲、乙兩種電子鐘走時誤差的平均數;
(2) 計算甲、乙兩種電子鐘走時誤差的方差;
(3) 根據經驗,走時穩定性較好的電子鐘質量更優.若兩種類型的電子鐘價格相同,請問:你買哪種電子鐘?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市某童裝專賣店在銷售中發現,一款童裝每件進價為40元,若銷售價為60元,每天可售出20件,為迎接“雙十一”,專賣店決定采取適當的降價措施,以擴大銷售量,經市場調查發現:如果每件童裝降價1元,那么平均可多售出2件,設每件童裝降價x元(x>0)時,平均每天可盈利y元.
(1)寫出y與x的函數關系式;
(2)根(1)中你寫出的函數關系式,解答下列問題:
①當該專賣店每件童裝降價5元時,平均每天盈利多少元?
②當該專賣店每件童裝降價多少元時,平均每天盈利400元?
③該專賣店要想平均每天盈利600元,可能嗎?請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(12分)某中學組織學生去福利院慰問,在準備禮品時發現,購買1個甲禮品比購買1個乙禮品多花40元,并且花費600元購買甲禮品和花費360元購買乙禮品的數量相等.
(1)求甲、乙兩種禮品的單價各為多少元?
(2)學校準備購買甲、乙兩種禮品共30個送給福利院的老人,要求購買禮品的總費用不超過2000元,那么最多可購買多少個甲禮品?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 、
、![]() 兩地相距
兩地相距![]() ,甲、乙兩車分別沿同一條路線從
,甲、乙兩車分別沿同一條路線從![]() 地出發駛往
地出發駛往![]() 地,已知甲車的速度為
地,已知甲車的速度為![]() ,乙車的速度為
,乙車的速度為![]() ,甲車先出發
,甲車先出發![]() 后乙車再出發,乙車到達
后乙車再出發,乙車到達![]() 地后再原地等甲車.
地后再原地等甲車.
(1)求乙車出發多長時間追上甲車?
(2)求乙車出發多長時間與甲車相距![]() ?
?
查看答案和解析>>
科目:初中數學 來源: 題型:
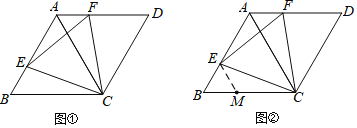
【題目】如圖,在菱形ABCD中,∠B= 60°.
(1)如圖①.若點E、F分別在邊AB、AD上,且BE=AF,求證:△CEF是等邊三角形.
(2)小明發現,當點E、F分別在邊AB、AD上,且∠CEF=60°時,△CEF也是等邊三角形,
并通過畫圖驗證了猜想;小麗通過探索,認為應該以CE= EF為突破口,構造兩個全等三角形:小倩受到小麗的啟發,嘗試在BC上截取BM =BE,并連接ME,如圖②,很快就證明了△CEF是等邊三角形.請你根據小倩的方法,寫出完整的證明過程.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在樓房MN前有兩棵樹與樓房在同一直線上,且垂直于地面,為了測量樹AB、CD的高度,小明爬到樓房頂部M處,光線恰好可以經過樹CD的頂站C點到達樹AB的底部B點,俯角為37°,此時小亮測得太陽光線恰好經過樹CD的頂部C點到達樓房的底部N點,與地面的夾角為30°,樹CD的影長DN為15米,請求出樹AB和樓房MN的高度.
(![]() ,
,![]() ,
,![]() ,
,![]() ,結果精確到0.1m)
,結果精確到0.1m)

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com