
【題目】綜合與實踐﹣﹣旋轉中的數學
問題背景:在一次綜合實踐活動課上,同學們以兩個矩形為對象,研究相似矩形旋轉中的問題:已知矩形ABCD∽矩形A′B′C′D′,它們各自對角線的交點重合于點O,連接AA′,CC′.請你幫他們解決下列問題:
觀察發現:(1)如圖1,若A′B′∥AB,則AA′與CC′的數量關系是______;
操作探究:(2)將圖1中的矩形ABCD保持不動,矩形A′B′C′D′繞點O逆時針旋轉角度α(0°<α≤90°),如圖2,在矩形A′B′C′D′旋轉的過程中,(1)中的結論還成立嗎?若成立,請證明;若不成立,請說明理由;
操作計算:(3)如圖3,在(2)的條件下,當矩形A′B′C′D′繞點O旋轉至AA′⊥A′D′時,若AB=6,BC=8,A′B′=3,求AA′的長.

【答案】AA′=CC′
【解析】
(1)連接AC、A′C′,根據題意得到點A、A′、C′、C在同一條直線上,根據矩形的性質得到OA=OC,OA′=OC′,得到答案;
(2)連接AC、A′C′,證明△A′OA≌△C′OC,根據全等三角形的性質證明;
(3)連接AC,過C作CE⊥AB′,交AB′的延長線于E,根據相似多邊形的性質求出B′C′,根據勾股定理計算即可.
(1)AA′=CC′,
理由如下:連接AC、A′C′,
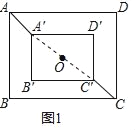
∵矩形ABCD∽矩形A′B′C′D′,∠CAB=∠C′A′B′,
∵A′B′∥AB,
∴點A、A′、C′、C在同一條直線上,
由矩形的性質可知,OA=OC,OA′=OC′,
∴AA′=CC′,
故答案為:AA′=CC′;
(2)(1)中的結論還成立,AA′=CC′,
理由如下:連接AC、A′C′,則AC、A′C′都經過點O,
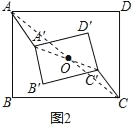
由旋轉的性質可知,∠A′OA=∠C′OC,
∵四邊形ABCD和四邊形A′B′C′D′都是矩形,
∴OA=OC,OA′=OC′,
在△A′OA和△C′OC中,
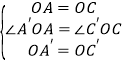 ,
,
∴△A′OA≌△C′OC,
∴AA′=CC′;
(3)連接AC,過C作CE⊥AB′,交AB′的延長線于E,
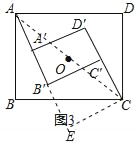
∵矩形ABCD∽矩形A′B′C′D′,
∴![]() ,即
,即![]() ,
,
解得,B′C′=4,
∵∠EB′C=∠B′C′C=∠E=90°,
∴四邊形B′ECC′為矩形,
∴EC=B′C′=4,
在Rt△ABC中,AC=![]() =10,
=10,
在Rt△AEC中,AE=![]() =2
=2![]() ,
,
∴AA′+B′E=2![]() ﹣3,又AA′=CC′=B′E,
﹣3,又AA′=CC′=B′E,
∴AA′=![]() .
.


 單元期中期末卷系列答案
單元期中期末卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,∠ACB=90°,OC=2BO,AC=6,點B的坐標為(1,0),拋物線y=﹣x2+bx+c經過A、B兩點.
(1)求點A的坐標;
(2)求拋物線的解析式;
(3)點P是直線AB上方拋物線上的一點,過點P作PD垂直x軸于點D,交線段AB于點E,使PE=![]() DE.
DE.
①求點P的坐標;
②在直線PD上是否存在點M,使△ABM為直角三角形?若存在,求出符合條件的所有點M的坐標;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商家用1200元購進了一批T恤,上市后很快售完,商家又用2800元購進了第二批這種T恤,所購數量是第一批購進量的2倍,但單價貴了5元.
(1)該商家購進的第一批T恤是多少件?
(2)若兩批T恤按相同的標價銷售,最后剩下20件按八折優惠賣出,如果希望兩批T恤全部售完的利潤率不低于16%(不考慮其它因素),那么每件T恤的標價至少是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已如:⊙O與⊙O上的一點A
(1)求作:⊙O的內接正六邊形ABCDEF;( 要求:尺規作圖,不寫作法但保留作圖痕跡)
(2)連接CE,BF,判斷四邊形BCEF是否為矩形,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是某旅游景點的一處臺階,其中臺階坡面AB和BC的長均為6m,AB部分的坡角∠BAD為45°,BC部分的坡角∠CBE為30°,其中BD⊥AD,CE⊥BE,垂足為D,E.現在要將此臺階改造為直接從A至C的臺階,如果改造后每層臺階的高為22cm,那么改造后的臺階有多少層?(最后一個臺階的高超過15cm且不足22cm時,按一個臺階計算.可能用到的數據:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,直線![]() 交
交![]() 軸于點
軸于點![]() ,交
,交![]() 軸于點
軸于點![]() ,以
,以![]() 為邊作正方形
為邊作正方形![]() ,請解決下列問題:
,請解決下列問題:
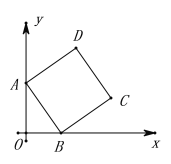
(1)求點![]() 和點
和點![]() 的坐標;
的坐標;
(2)求直線![]() 的解析式;
的解析式;
(3)在直線![]() 上是否存在點
上是否存在點![]() ,使
,使![]() 為等腰三角形?若存在,請直接寫出點
為等腰三角形?若存在,請直接寫出點![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綜合與實踐
(1)問題發現

如圖1,![]() 和
和![]() 均為等邊三角形,點
均為等邊三角形,點![]() 在同一直線上,連接
在同一直線上,連接![]() .請寫出
.請寫出![]() 的度數及線段
的度數及線段![]() 之間的數量關系,并說明理由.
之間的數量關系,并說明理由.
(2)類比探究
如圖2,![]() 和
和![]() 均為等腰直角三角形,
均為等腰直角三角形,![]() ,點
,點![]() 在同一直線上,
在同一直線上,![]() 為
為![]() 中
中![]() 邊上的高,連接
邊上的高,連接![]() .
.
填空:①![]() 的度數為____________;
的度數為____________;
②線段![]() 之間的數量關系為_______________________________.
之間的數量關系為_______________________________.
(3)拓展延伸
在(2)的條件下,若![]() ,則四邊形
,則四邊形![]() 的面積為______________.
的面積為______________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是反比例函數![]() 的圖象的一個分支.
的圖象的一個分支.
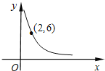
![]() 比例系數
比例系數![]() 的值是________;
的值是________;
![]() 寫出該圖象的另一個分支上的
寫出該圖象的另一個分支上的![]() 個點的坐標:________、________;
個點的坐標:________、________;
![]() 當
當![]() 在什么范圍取值時,
在什么范圍取值時,![]() 是小于
是小于![]() 的正數?
的正數?
![]() 如果自變量
如果自變量![]() 取值范圍為
取值范圍為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“垃圾分類”意識已經深入人心.我校王老師準備用![]() 元(全部用完)購買
元(全部用完)購買![]() 兩類垃圾桶,已知
兩類垃圾桶,已知![]() 類桶單價
類桶單價![]() 元,
元,![]() 類桶單價
類桶單價![]() 元,設購入
元,設購入![]() 類桶
類桶![]() 個,
個,![]() 類桶
類桶![]() 個.
個.
(1)求![]() 關于
關于![]() 的函數表達式.
的函數表達式.
(2)若購進的![]() 類桶不少于
類桶不少于![]() 類桶的
類桶的![]() 倍.
倍.
①求至少購進![]() 類桶多少個?
類桶多少個?
②根據臨場實際購買情況,王老師在總費用不變的情況下把一部分![]() 類桶調換成另一種
類桶調換成另一種![]() 類桶,且調換后
類桶,且調換后![]() 類桶的數量不少于
類桶的數量不少于![]() 類桶的數量,已知
類桶的數量,已知![]() 類桶單價
類桶單價![]() 元,則按這樣的購買方式,
元,則按這樣的購買方式,![]() 類桶最多可買 個.(直接寫出答案)
類桶最多可買 個.(直接寫出答案)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com