
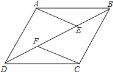
【題目】如圖,E,F是四邊形ABCD的對角線BD上的兩點,AE∥CF,AB∥CD,BE=DF,則下列結(jié)論:
①AE=CF,②AD=BC,③AD∥BC,④∠BCF=∠DAE,
其中正確的個數(shù)為( )
A.1個B.2個C.3個D.4個
科目:初中數(shù)學 來源: 題型:
【題目】閱讀與思考;
婆羅摩笈多是一位印度數(shù)學家與天文學家,書寫了兩部關(guān)于數(shù)學與天文的書籍,他的一些數(shù)學成就在世界數(shù)學史上有較高的地位,他的負數(shù)及加減法運算僅晚于中國九章算術(shù)而他的負數(shù)乘除法法則在全世界都是領(lǐng)先的,他還提出了著名的婆羅摩笈多定理,該定理的內(nèi)容及證明如下:
已知:如圖,四邊形ABCD內(nèi)接與圓O對角線AC⊥BD于點M,ME⊥BC于點E,延長EM交CD于F,求證:MF=DF
證明∵AC⊥BD,ME⊥BC
∴∠CBD=∠CME
∵∠CBD=∠CAD,∠CME=∠AMF
∴∠CAD=∠AMF
∴AF=MF
∵∠AMD=90°,同時∠MAD+∠MDA=90°
∴∠FMD=∠FDM
∴MF=DF,即F是AD中點.
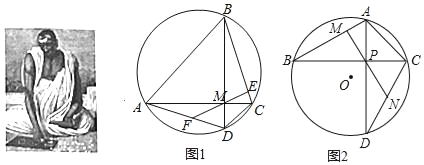
(1)請你閱讀婆羅摩笈多定理的證明過程,完成婆羅摩笈多逆定理的證明:
已知:如圖1,四邊形ABCD內(nèi)接與圓O,對角線AC⊥BD于點M,F是AD中點,連接FM并延長交BC于點E,求證:ME⊥BC
(2)已知如圖2,△ABC內(nèi)接于圓O,∠B=30°∠ACB=45°,AB=2,點D在圓O上,∠BCD=60°,連接AD 交BC于點P,作ON⊥CD于點N,延長NP交AB于點M,求證PM⊥BA并求PN的長.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知:⊙O為Rt△ABC的外接圓,點D在邊AC上,AD=AO;
(1)如圖1,若弦BE∥OD,求證:OD=BE;
(2)如圖2,點F在邊BC上,BF=BO,若OD=2![]() , OF=3,求⊙O的直徑.
, OF=3,求⊙O的直徑.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】有若干個數(shù),第一個記為![]() ,第二個記為
,第二個記為![]() ,第三個記為
,第三個記為![]() …. 若
…. 若![]() ,從第2個數(shù)起,每個數(shù)都等于“1與它前面那個數(shù)的差的倒數(shù)”.
,從第2個數(shù)起,每個數(shù)都等于“1與它前面那個數(shù)的差的倒數(shù)”.
(1)計算![]() 的值.
的值.
(2)根據(jù)以上計算結(jié)果,直接寫出![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】![]() 三點在數(shù)軸上,點
三點在數(shù)軸上,點![]() 表示的數(shù)是
表示的數(shù)是![]() ,從點
,從點![]() 出發(fā)向右平移7個單位長度得到點
出發(fā)向右平移7個單位長度得到點![]() 。
。
(1)求出點![]() 表示的數(shù),畫一條數(shù)軸并在數(shù)軸上標出點
表示的數(shù),畫一條數(shù)軸并在數(shù)軸上標出點![]() 和點
和點![]() ;
;
(2)若此數(shù)軸在一張紙上,將紙沿某一條直線對折,此時![]() 點與表示數(shù)
點與表示數(shù)![]() 的點剛好重合,折痕與數(shù)軸有一個交點
的點剛好重合,折痕與數(shù)軸有一個交點![]() ,求點
,求點![]() 表示的數(shù)的相反數(shù)(原卷無此問);
表示的數(shù)的相反數(shù)(原卷無此問);
(3)在數(shù)軸上有一點![]() ,點
,點![]() 到點
到點![]() 和點
和點![]() 的距離之和為11,求點
的距離之和為11,求點![]() 所表示的數(shù);
所表示的數(shù);
(4)![]() 從初始位置分別以1單位長度
從初始位置分別以1單位長度![]() 和2單位長度
和2單位長度![]() 的速度同時向左運動,是否存在
的速度同時向左運動,是否存在![]() 的值,使
的值,使![]() 秒后點
秒后點![]() 到
到![]() 的距離與點
的距離與點![]() 到原點距離相等?若存在請求出
到原點距離相等?若存在請求出![]() 的值;若不存在,請說明理由。
的值;若不存在,請說明理由。
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】一文體用品商店為吸引中學生顧客,在店內(nèi)出示了一道數(shù)學題,凡是能正確解答這道題的,店內(nèi)商品一律給該生9折優(yōu)惠或每購滿10元立減3元(不足10元部分不減)優(yōu)惠方式.題目是這樣的:購一個筆盒和2個羽毛球共需26元,買2個筆盒和一個羽毛球共需37元,
(1)請列方程或方程組解答商家提出的問題;問:筆盒與羽毛球的單價各是多少元?
(2)一位同學回答對了問題,他想購買羽毛球和筆盒各一個,請列舉能享受到優(yōu)惠的購買方式,并幫助他選擇一種最優(yōu)惠的購買方式.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,是一塊在電腦屏幕上出現(xiàn)的長方形色塊圖,由6個不同的正方形組成。設(shè)中間最小的一個正方形邊長為1,則這個長方形色塊圖的面積為_____________.

查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com