
【題目】教室里的飲水機接通電源就進入自動程序,開機加熱時每分鐘上升10℃,加熱到100℃,停止加熱,水溫開始下降,此時水溫(℃)與開機后用時(min)成反比例關系.直至水溫降至30℃,飲水機關機.飲水機關機后即刻自動開機,重復上述自動程序.若在水溫為30℃時,接通電源后,水溫y(℃)和時間(min)的關系如圖,為了在上午第一節下課時(8:45)能喝到不超過50℃的水,則接通電源的時間可以是當天上午的( )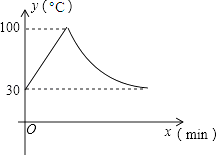
A.7:20
B.7:30
C.7:45
D.7:50
【答案】A
【解析】解:∵開機加熱時每分鐘上升10℃,
∴從30℃到100℃需要7分鐘,
設一次函數關系式為:y=k1x+b,
將(0,30),(7,100)代入y=k1x+b得k1=10,b=30
∴y=10x+30(0≤x≤7),令y=50,解得x=2;
設反比例函數關系式為:y= ![]() ,
,
將(7,100)代入y= ![]() 得k=700,∴y=
得k=700,∴y= ![]() ,
,
將y=30代入y= ![]() ,解得x=
,解得x= ![]() ;
;
∴y= ![]() (7≤x≤
(7≤x≤ ![]() ),令y=50,解得x=14.
),令y=50,解得x=14.
所以,飲水機的一個循環周期為 ![]() 分鐘.每一個循環周期內,在0≤x≤2及14≤x≤
分鐘.每一個循環周期內,在0≤x≤2及14≤x≤ ![]() 時間段內,水溫不超過50℃.
時間段內,水溫不超過50℃.
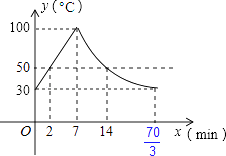
逐一分析如下:
選項A:7:20至8:45之間有85分鐘.85﹣ ![]() ×3=15,位于14≤x≤
×3=15,位于14≤x≤ ![]() 時間段內,故可行;
時間段內,故可行;
選項B:7:30至8:45之間有75分鐘.75﹣ ![]() ×3=5,不在0≤x≤2及14≤x≤
×3=5,不在0≤x≤2及14≤x≤ ![]() 時間段內,故不可行;
時間段內,故不可行;
選項C:7:45至8:45之間有60分鐘.60﹣ ![]() ×2=
×2= ![]() ≈13.3,不在0≤x≤2及14≤x≤
≈13.3,不在0≤x≤2及14≤x≤ ![]() 時間段內,故不可行;
時間段內,故不可行;
選項D:7:50至8:45之間有55分鐘.55﹣ ![]() ×2=
×2= ![]() ≈8.3,不在0≤x≤2及14≤x≤
≈8.3,不在0≤x≤2及14≤x≤ ![]() 時間段內,故不可行.
時間段內,故不可行.
綜上所述,四個選項中,唯有7:20符合題意.
故答案為:A.
根據實際情況由開機加熱時每分鐘上升10℃,得到從30℃到100℃需要7分鐘,設出一次函數關系式為y=k1x+b,將(0,30),(7,100)代入y=k1x+bk1=10,求出b=30,解得x=2;設反比例函數關系式為y= ![]() ,將(7,100)代
,將(7,100)代![]() 入得k=700,得到解析式
入得k=700,得到解析式![]() ,求出飲水機的一個循環周期為的時間,每一個循環周期內,分時間段分析,得出結論.
,求出飲水機的一個循環周期為的時間,每一個循環周期內,分時間段分析,得出結論.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,邊長分別為1和2的兩個等邊三角形,開始它們在左邊重合,大三角形固定不動,然后把小三角形自左向右平移直至移出大三角形外停止.設小三角形移動的距離為x,兩個三角形重疊面積為y,則y關于x的函數圖象是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】以下敘述正確的有( )
①對頂角相等;②同位角相等;③兩直角相等;④鄰補角相等;⑤多邊形的外角和都相等;⑥三角形的中線把原三角形分成面積相等的兩個三角形
A.2個B.3個C.4個D.5個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,貴陽市某中學數學活動小組在學習了“利用三角函數測高”后.選定測量小河對岸一幢建筑物BC的高度.他們先在斜坡上的D處,測得建筑物頂的仰角為30°.且D離地面的高度DE=5m.坡底EA=10m,然后在A處測得建筑物頂B的仰角是50°,點E,A,C在同一水平線上,求建筑物BC的高.(結果保留整數)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,M是△ABC的邊BC的中點,AN平分∠BAC,BN⊥AN于點N,延長BN交AC于點D,已知AB=10,BC=15,MN=3
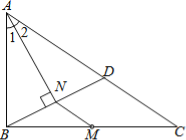
(1)求證:BN=DN;
(2)求△ABC的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△PQR是⊙O的內接正三角形,四邊形ABCD是⊙O的內接正方形,BC∥QR,則∠AOQ=( )
A.60°
B.65°
C.72°
D.75°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某同學在![]() ,
,![]() 兩家超市發現他看中的隨身聽的單價相同,書包單價也相同,隨身聽和書包單價之和是
兩家超市發現他看中的隨身聽的單價相同,書包單價也相同,隨身聽和書包單價之和是![]() 元,且隨身聽的單價比書包的單價的
元,且隨身聽的單價比書包的單價的![]() 倍少
倍少![]() 元.
元.
(1)求該同學看中的隨身聽和書包的單價各是多少元?
(2)某一天該同學上街,恰好趕上商家促銷,超市![]() 所有商品打八五折銷售,超市
所有商品打八五折銷售,超市![]() 全場購物每滿
全場購物每滿![]() 元返購物券
元返購物券![]() 元銷售(不足
元銷售(不足![]() 元不返券,購物券全場通用),但他只帶了
元不返券,購物券全場通用),但他只帶了![]() 元錢,如果他只在一家超市購買看中的這兩樣商品,你能說明他可以選擇哪一家購買嗎?若兩家都可以選擇,在哪一家購買更省錢?
元錢,如果他只在一家超市購買看中的這兩樣商品,你能說明他可以選擇哪一家購買嗎?若兩家都可以選擇,在哪一家購買更省錢?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,AD是△ABC的角平分線,DE⊥AB,DF⊥AC,垂足分別為E,F.則下列結論:①AD上任意一點到點C,B的距離相等;②AD上任意一點到邊AB,AC的距離相等;③BD=CD,AD⊥BC;④∠BDE=∠CDF.其中正確的個數為( )

A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中數學 來源: 題型:
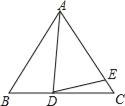
【題目】已知△ABC,AB=AC,D為BC上一點,E為AC上一點,AD=AE.
(1)如果∠BAD=10°,∠DAE=30°,那么∠EDC= °.
(2)如果∠ABC=60°,∠ADE=70°,那么∠BAD= °,∠CDE= °.
(3)設∠BAD=α,∠CDE=β猜想α,β之間的關系式,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com