
【題目】如圖8,點D是⊙O的直徑CA延長線上一點,點B在⊙O上,且AB=AD=AO.
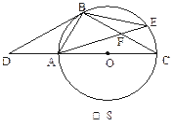
(1)求證:BD是⊙O的切線.
(2)若點E是劣弧BC上一點,AE與BC相交于點F,且△BEF的面積為8,cos∠BFA=![]() ,求△ACF的面積.
,求△ACF的面積.
 培優好卷單元加期末卷系列答案
培優好卷單元加期末卷系列答案科目:初中數學 來源: 題型:
【題目】為了解某校九年級男生的體能情況,體育老師從中隨機抽取部分男生進行引體向上測試,并對成績進行了統計,繪制成尚不完整的扇形圖和條形圖,根據圖形信息回答下列問題:
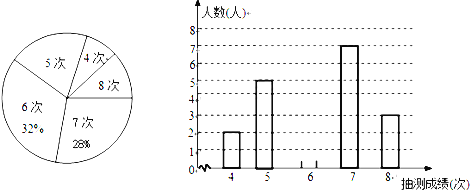
(1)本次抽測的男生有________人,抽測成績的眾數是_________;
(2)請將條形圖補充完整;
(3)若規定引體向上6次以上(含6次)為體能達標,則該校125名九年級男生中估計有多少人體能達標?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線![]() 過點A(m-2,n), B(m+4,n),C(m,
過點A(m-2,n), B(m+4,n),C(m,![]() ).
).
(1)b=__________(用含m的代數式表示);
(2)求△ABC的面積;
(3)當![]() 時,均有
時,均有![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,點F在AD上,點E在BC上,把矩形沿EF折疊后,使點D恰好落 在BC邊上的G點處,若矩形面積為![]() 且∠AFG=60°,GE=2BG,則折痕EF的長為( )
且∠AFG=60°,GE=2BG,則折痕EF的長為( )

A.1B.![]() C.2D.
C.2D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知二次函數![]() 的圖象與
的圖象與![]() 軸交于點
軸交于點![]() 、
、![]() ,與
,與![]() 軸交于點
軸交于點![]() .
.
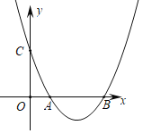
(1)求二次函數的解析式;
(2)若點![]() 為拋物線上的一點,點
為拋物線上的一點,點![]() 為對稱軸上的一點,且以點
為對稱軸上的一點,且以點![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形為平行四邊形,求點
為頂點的四邊形為平行四邊形,求點![]() 的坐標;
的坐標;
(3)點![]() 是二次函數第四象限圖象上一點,過點
是二次函數第四象限圖象上一點,過點![]() 作
作![]() 軸的垂線,交直線
軸的垂線,交直線![]() 于點
于點![]() ,求四邊形
,求四邊形![]() 面積的最大值及此時點
面積的最大值及此時點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料,并完成相應任務.
 古希臘數學家,天文學家歐多克索斯(Eudoxus,約前400—前347)曾提出:能否將一
古希臘數學家,天文學家歐多克索斯(Eudoxus,約前400—前347)曾提出:能否將一
條線段分成不相等的兩部分.使較短線段與較長線段的比等于較長線段與原線段的比,這個相等的比就是![]() ,黃金分割在我們生活中有廣泛運用.黃金分割點也可以用折紙的方式得到.
,黃金分割在我們生活中有廣泛運用.黃金分割點也可以用折紙的方式得到.
第一步:裁一張正方形的紙片![]() ,先折出
,先折出![]() 的中點
的中點![]() ,然后展平,再折出線段
,然后展平,再折出線段![]() ,再展平;
,再展平;
第二步:將紙片沿![]() 折疊,使
折疊,使![]() 落到線段
落到線段![]() 上,
上,![]() 的對應點為
的對應點為![]() ,展平;
,展平;
第三步:沿![]() 折疊,使
折疊,使![]() 落在
落在![]() 上,
上,![]() 的對應點為
的對應點為![]() ,展平,這時
,展平,這時![]() 就是
就是![]() 的黃金分割點.
的黃金分割點.

 古希臘數學家,天文學家歐多克索斯(Eudoxus,約前400—前347)曾提出:能否將一
古希臘數學家,天文學家歐多克索斯(Eudoxus,約前400—前347)曾提出:能否將一
條線段分成不相等的兩部分.使較短線段與較長線段的比等于較長線段與原線段的比,這個相等的比就是![]() ,黃金分割在我們生活中有廣泛運用.黃金分割點也可以用折紙的方式得到.
,黃金分割在我們生活中有廣泛運用.黃金分割點也可以用折紙的方式得到.
第一步:裁一張正方形的紙片![]() ,先折出
,先折出![]() 的中點
的中點![]() ,然后展平,再折出線段
,然后展平,再折出線段![]() ,再展平;
,再展平;
第二步:將紙片沿![]() 落到線段
落到線段![]() 上,
上,![]() 的對應點為
的對應點為![]() ,展平;
,展平;
第三步:沿![]() 折疊,使
折疊,使![]() 落在
落在![]() 上,
上,![]() 的對應點為
的對應點為![]() ,展平,這時
,展平,這時![]() 就是
就是![]() 的黃金分割點.
的黃金分割點.

任務:(1)試根據以上操作步驟證明![]() 就是
就是![]() 的黃金分割點;
的黃金分割點;
(2)請寫出一個生活中應用黃金分割的實際例子.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點O是邊長為4的等邊三角形ABC的中心,∠EOF的兩邊與△ABC的邊AB,BC分別交于E、F,∠EOF=120°.
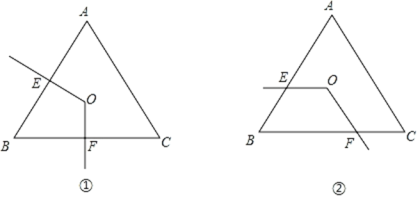
(1)如圖①,當E為AB中點時,求∠EOF與△ABC的邊所圍成的四邊形OEBF的面積;
(2)如圖②,∠EOF繞點O旋轉.在旋轉過程中四邊形OEBF的面積會改變嗎?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,己知拋物線![]() 與
與![]() 軸相交于點
軸相交于點![]() ,其對稱軸與拋物線相交于點
,其對稱軸與拋物線相交于點![]() ,與
,與![]() 軸相交于點
軸相交于點![]() .
.
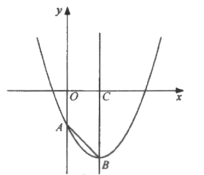
(1)求![]() 的長;
的長;
(2)平移該拋物線得到一條新拋物線,設新拋物線的頂點為![]() .若新拋物線經過原點
.若新拋物線經過原點![]() ,且
,且![]() ,求新拋物線對應的函數表達式.
,求新拋物線對應的函數表達式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com