
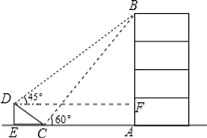
【題目】如圖,在大樓AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小紅在斜坡下的點C處測得樓頂B的仰角為60°,在斜坡上的點D處測得樓頂B的仰角為45°,其中點A、C、E在同一直線上.

(1)求斜坡CD的高度DE;
(2)求大樓AB的高度(結果保留根號)
【答案】(1)2米;(2)(6+![]() )或(6-
)或(6-![]() )米.
)米.
【解析】試題分析:(1)在在Rt△DCE中,利用30°所對直角邊等于斜邊的一半,可求出DE=2米;(2)過點D作DF⊥AB于點F,則AF=2,根據三角函數可用BF表示BC、BD,然后可判斷△BCD是Rt△,進而利用勾股定理可求得BF的長,AB的高度也可求.
試題解析:(1)在Rt△DCE中,∠DEC=90°,∠DCE=30°,∴DE=![]() DC=2米;(2)過D作DF⊥AB,交AB于點F,則AF=DE=2米.∵∠BFD=90°,∠BDF=45°,∴∠BFD=45°,∴BF=DF.設BF=DF=x米,則AB=(x+2)米,在Rt△ABC中,∠BAC=90°,∠BCA=60°,∴sin∠BCA=
DC=2米;(2)過D作DF⊥AB,交AB于點F,則AF=DE=2米.∵∠BFD=90°,∠BDF=45°,∴∠BFD=45°,∴BF=DF.設BF=DF=x米,則AB=(x+2)米,在Rt△ABC中,∠BAC=90°,∠BCA=60°,∴sin∠BCA=![]() ,∴BC=AB÷sin∠BCA=(x+2)÷
,∴BC=AB÷sin∠BCA=(x+2)÷![]() =
=![]() 米,在Rt△BDF中,∠BFD=90°,
米,在Rt△BDF中,∠BFD=90°,![]() 米,∵∠DCE=30°,∠ACB=60°,∴∠DCB=90°.∴
米,∵∠DCE=30°,∠ACB=60°,∴∠DCB=90°.∴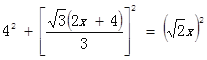 ,解得:x=4+
,解得:x=4+![]() 或x=4﹣
或x=4﹣![]() ,則AB=(6+
,則AB=(6+![]() )米或(6﹣
)米或(6﹣![]() )米.
)米.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】實踐探究題
(1)![]() 是不為1的有理數,我們把
是不為1的有理數,我們把![]() 稱為
稱為![]() 的差倒數.如:2的差倒數是
的差倒數.如:2的差倒數是![]() ,
, ![]() 的差倒數是
的差倒數是![]() .已知
.已知![]() ,
, ![]() 是
是![]() 的差倒數,
的差倒數, ![]() 是
是![]() 的差倒數,
的差倒數, ![]() 是
是![]() 的差倒數,…,依此類推,
的差倒數,…,依此類推, ![]() 的差倒數
的差倒數![]() ________.
________.
(2)觀察下列有規律的數: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() …根據規律可知:
…根據規律可知:
①第10個數是________, ![]() 是第________個數.
是第________個數.
②計算![]() ________.(直接寫出答案即可)
________.(直接寫出答案即可)
(3)高斯函數[x],也稱為取整函數,即[x]表示不超過x的最大整數.
例如:[2.3]=2,[-1.5]=-2.
則下列結論:①[-2.1]+[1]=-2;②[x]+[-x]=0;③[2.5]+[-2.5]=-1; ④[x+1]+[-x+1]的值為2.
其中正確的結論有________ (填序號).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校想了解學生每周的課外閱讀時間情況,隨機調查了部分學生,對學生每周的課外閱讀時間x(單位:小時)進行分組整理,并繪制了如圖所示的不完整的頻數分布直方圖和扇形統計圖: 
根據圖中提供的信息,解答下列問題:
(1)共隨機調查了名學生,課外閱讀時間在6﹣8小時之間有人,并補全頻數分布直方圖
(2)求扇形統計圖中m的值和E組對應的圓心角度數;
(3)請估計該校3000名學生每周的課外閱讀時間不小于6小時的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】實驗初中有A、B兩個閱覽室,甲、乙、丙三名學生各自隨機選擇其中的一個閱覽室閱讀.
下列事件中,是必然事件的為( )
A.甲、乙同學都在A閱覽室;B.甲、乙、丙同學中至少兩人在A閱覽室;
C.甲、乙同學在同一閱覽室D.甲、乙、丙同學中至少兩人在同一閱覽室
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店準備購進一批季節性小家電,單價40元,經市場預測,銷售定價為52元時,可售出180個。定價每增加1元,銷售量凈減少10個;定價每減少1元,銷售量凈增加10個。因受庫存的影響,每批次進貨個數不得超過180個。商店若準備獲利2000元,則應進貨多少個?定價多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】判定一個三角形是不是等腰三角形,我們經常利用以下的判定方法:“如果一個三角形有兩個角相等,那么這兩個角所對的邊也相等”,請你利用以上判定方法解決下列問題
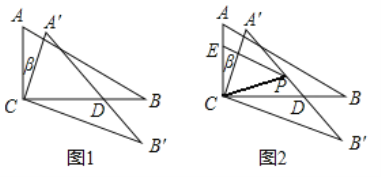
如圖1,在△ABC中,∠ACB=90°,∠B=30°,將△ABC繞頂點C順時針旋轉,旋轉角為β
(0°<β<180°),得到△A′B′C
(1)設A′B′與CB相交于點D,
①當旋轉角為β=25°,∠B′DB= °;
②當AB∥CB′ 時,求證:D是A′B′ 的中點;
(2)如圖2,E是AC邊上的點,且![]() ,P是A′B′邊上的點,且∠A′PC=60°,連接EP、CP,已知AC=10,①當β= °時,EP長度最大,最大值為 ;
,P是A′B′邊上的點,且∠A′PC=60°,連接EP、CP,已知AC=10,①當β= °時,EP長度最大,最大值為 ;
②當β= °時,△ECP的面積最大,最大值為 。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com