
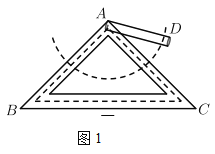
【題目】我們把兩條中線互相垂直的三角形稱為“中垂三角形”. 如圖1,圖2,圖3中,![]() 是
是![]() 的中線,
的中線,![]() ,垂足為點
,垂足為點![]() ,像
,像![]() 這樣的三角形均為“中垂三角形. 設
這樣的三角形均為“中垂三角形. 設![]() .
.
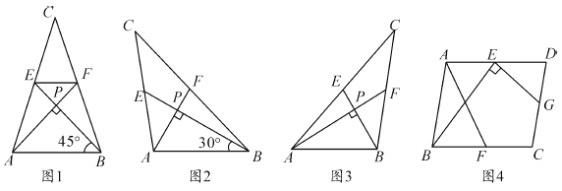
(1)如圖1,當![]() 時,則
時,則![]() _________,
_________,![]() __________;
__________;
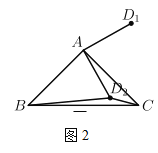
(2)如圖2,當![]() 時,則
時,則![]() _________,
_________,![]() __________;
__________;
歸納證明
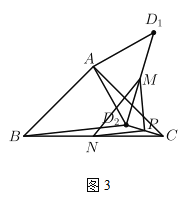
(3)請觀察(1)(2)中的計算結果,猜想![]() 三者之間的關系,用等式表示出來,并利用圖3證明你發現的關系式;
三者之間的關系,用等式表示出來,并利用圖3證明你發現的關系式;
拓展應用
(4)如圖4,在![]() 中,
中,![]() 分別是
分別是![]() 的中點,且
的中點,且![]() . 若
. 若![]() ,
,![]() ,求
,求![]() 的長.
的長.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]() ,證明見解析;(4)
,證明見解析;(4)![]()
【解析】
(1)根據三角形的中位線得出;![]() ,進而得到
,進而得到![]() 計算即可得出答案;
計算即可得出答案;
(2)連接EF,中位線的性質以及![]() 求出AP、BP、EP和FP的長度再根據勾股定理求出AE和BF的長度即可得出答案;
求出AP、BP、EP和FP的長度再根據勾股定理求出AE和BF的長度即可得出答案;
(3)連接EF,根據中位線的性質得出![]() ,根據勾股定理求出AE與AP和EP的關系以及BF與BP和FP的關系,即可得出答案;
,根據勾股定理求出AE與AP和EP的關系以及BF與BP和FP的關系,即可得出答案;
(4)取![]() 的中點
的中點![]() ,連接
,連接![]() ,結合題目求出四邊形
,結合題目求出四邊形![]() 是平行四邊形得出AP=FP即可得到
是平行四邊形得出AP=FP即可得到![]() 是“中垂三角形”,根據第三問得出的結論代入,即可得出答案(連接
是“中垂三角形”,根據第三問得出的結論代入,即可得出答案(連接![]() ,交于點
,交于點![]() ,證明
,證明![]() 求得
求得![]() 是
是![]() 的中線,進而得出
的中線,進而得出![]() 是“中垂三角形”,再結合第三問得出的結論計算即可得出答案).
是“中垂三角形”,再結合第三問得出的結論計算即可得出答案).
解:(1)∵![]() 是
是![]() 的中線,∴
的中線,∴![]() 是
是![]() 的中位線,
的中位線,
∴![]() ,且
,且![]() ,易得
,易得![]() .
.
∵![]() ,
,
∴![]() ,∴
,∴![]() .
.
由勾股定理,得![]() ,
,
∴![]() .
.
(2)如圖2,連結![]() .
.
∵![]() 是
是![]() 的中線,
的中線,
∴![]() 是
是![]() 的中位線,
的中位線,
∴![]() ,且
,且![]() ,易得
,易得![]() .
.
. ∵![]() ,
,
∴![]() ,
,
∴![]() .
.
由勾股定理,得![]() ,
,
∴![]() .
.
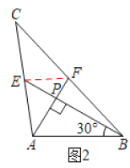
(3)![]() 之間的關系是
之間的關系是![]() .
.
證明如下:如圖3,連結![]() .
.

∵![]() 是
是![]() 的中線,
的中線,
∴![]() 是
是![]() 的中位線.
的中位線.
∴![]() ,且
,且![]() ,
,
易得![]() .
.
在![]() 和
和![]() 中,
中,
∵![]() ,
,![]() ,
,
∴ .
.
∴![]() .
.
∴ ,
,
即![]() .
.
(4)解法1:設![]() 的交點為
的交點為![]() . 如圖4,取
. 如圖4,取![]() 的中點
的中點![]() ,連接
,連接![]() .
.
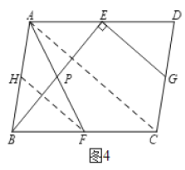
∵![]() 分別是
分別是![]() 的中點,
的中點,![]() 是
是![]() 的中點,
的中點,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∵四邊形![]() 是平行四邊形,
是平行四邊形,
∴![]() ,
,
∴![]() ,
,
∴四邊形![]() 是平行四邊形,
是平行四邊形,
∴![]() ,
,
∴![]() 是“中垂三角形”,
是“中垂三角形”,
∴![]() ,即
,即![]() ,
,
解得![]() .
.
(另:連接![]() ,交于點
,交于點![]() ,易得
,易得![]() 是“中垂三角形”,解法類似于解法1,如圖5)
是“中垂三角形”,解法類似于解法1,如圖5)

解法2:如圖6,連接![]() ,延長
,延長![]() 交
交![]() 的延長線于點
的延長線于點![]() .
.
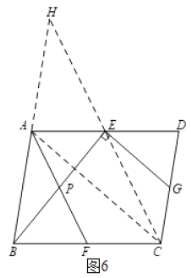
在![]() 中,∵
中,∵![]() 分別是
分別是![]() 的中點,
的中點,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
又∵四邊形![]() 為平行四邊形,
為平行四邊形,
∴![]() ,
,
易得![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是
是![]() 的中線,
的中線,
∴![]() 是“中垂三角形”,
是“中垂三角形”,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() ,
,
解得![]() .
.
∵![]() 是
是![]() 的中位線,
的中位線,
∴![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
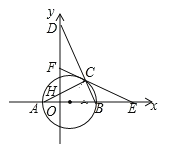
【題目】如圖,在平面直角坐標系中,△ABC內接于⊙P,AB是⊙P的直徑,A(﹣1,0)、C(3,2![]() ),BC的延長線交y軸于點D,點F是y軸上的一動點,連接FC并延長交x軸于點E.
),BC的延長線交y軸于點D,點F是y軸上的一動點,連接FC并延長交x軸于點E.
(1)求⊙P的半徑;
(2)當∠A=∠DCF時,求證:CE是⊙P的切線.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】A、B、C三人玩籃球傳球游戲,游戲規則是:第一次傳球由A將球隨機地傳給B,C兩人中的某一人,以后的每一次傳球都是由上次的傳球者隨機地傳給其他兩人中的某一人.
(1)求兩次傳球后,球恰在B手中的概率;
(2)求三次傳球后,球恰在A手中的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校一課外活動小組為了了解學生最喜歡的球類運動況,隨機抽查了本校九年級的200名學生,調查的結果如圖所示,請根據該扇形統計圖解答以下問題:
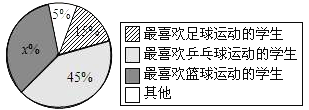
(1)圖中![]() 的值是________;
的值是________;
(2)被查的200名生中最喜歡球運動的學生有________人;
(3)若由3名最喜歡籃球運動的學生(記為![]() ),1名最喜歡乒乓球運動的學生(記為
),1名最喜歡乒乓球運動的學生(記為![]() ),1名最喜歡足球運動的學生(記為
),1名最喜歡足球運動的學生(記為![]() )組隊外出參加一次聯誼活動.欲從中選出2人擔任組長(不分正副),列出所有可能情況,并求2人均是最喜歡籃球運動的學生的概率.
)組隊外出參加一次聯誼活動.欲從中選出2人擔任組長(不分正副),列出所有可能情況,并求2人均是最喜歡籃球運動的學生的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著信息技術的迅猛發展,人們去商場購物的支付方式更加多樣、便捷.某校數學興趣小組設計了一份調查問卷,要求每人選且只選一種你最喜歡的支付方式.現將調查結果進行統計并繪制成如下兩幅不完整的統計圖,請結合圖中所給的信息解答下列問題:
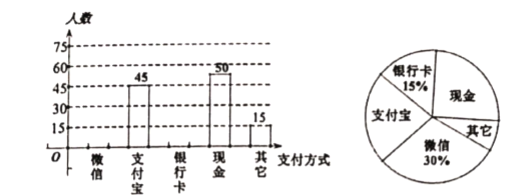
(1)這次活動共調查了多少人;
(2)將條形統計圖補充完整;
(3)在一次購物中,小明和小亮都想從“微信”、“支付寶”、“銀行卡”三種支付方式中選一種方式進行支付,請用畫樹狀圖或列表格的方法,求出兩人恰好選擇同一種支付方式的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1是實驗室中的一種擺動裝置,![]() 在地面上,支架
在地面上,支架![]() 是底邊為
是底邊為![]() 的等腰直角三角形,
的等腰直角三角形,![]() ,擺動臂
,擺動臂![]() 可繞點
可繞點![]() 旋轉,
旋轉,![]() .
.
(1)在旋轉過程中
①當![]() 、
、![]() 、
、![]() 三點在同一直線上時,求
三點在同一直線上時,求![]() 的長,
的長,
②當![]() 、
、![]() 、
、![]() 三點為同一直角三角形的頂點時,求
三點為同一直角三角形的頂點時,求![]() 的長.
的長.
(2)若擺動臂![]() 順時針旋轉
順時針旋轉![]() ,點
,點![]() 的位置由
的位置由![]() 外的點
外的點![]() 轉到其內的點
轉到其內的點![]() 處,如圖2,此時
處,如圖2,此時![]() ,
,![]() ,求
,求![]() 的長.
的長.
(3)若連接(2)中的![]() ,將(2)中
,將(2)中![]() 的形狀和大小保持不變,把
的形狀和大小保持不變,把![]() 繞點
繞點![]() 在平面內自由旋轉,分別取
在平面內自由旋轉,分別取![]() 、
、![]() 、
、![]() 的中點
的中點![]() 、
、![]() 、
、![]() ,連接
,連接![]() 、
、![]() 、
、![]() 、
、![]() 隨著
隨著![]() 繞點
繞點![]() 在平面內自由旋轉,
在平面內自由旋轉, ![]() 的面積是否發生變化,若不變,請直接寫出
的面積是否發生變化,若不變,請直接寫出![]() 的面積;若變化,
的面積;若變化,![]() 的面積是否存在最大與最小?若存在,請直接寫出
的面積是否存在最大與最小?若存在,請直接寫出![]() 面積的最大值與最小值,(溫馨提示
面積的最大值與最小值,(溫馨提示![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
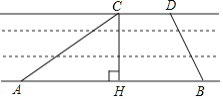
【題目】京杭大運河是世界文化遺產.綜合實踐活動小組為了測出某段運河的河寬(岸沿是平行的),如圖,在岸邊分別選定了點A、B和點C、D,先用卷尺量得AB=160m,CD=40m,再用測角儀測得∠CAB=30°,∠DBA=60°,求該段運河的河寬(即CH的長).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將含有 30°角的直角三角板 OAB 如圖放置在平面直角坐標系中,OB 在 x軸上,若 OA=2,將三角板繞原點 O 順時針旋轉 75°,則點 A 的對應點 A′ 的坐標為___________.
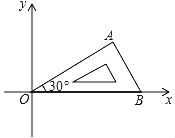
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】近年來,無人機航拍測量的應用越來越廣泛.如圖,無人機從A處觀測得某建筑物頂點O時俯角為30°,繼續水平前行10米到達B處,測得俯角為45°,已知無人機的水平飛行高度為45米,則這棟樓的高度是多少米?(結果保留根號)

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com