
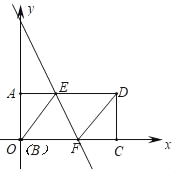
【題目】如圖,矩形ABCD中,AD=8,AB=4,將此矩形折疊,使點B與點D重合,折痕為EF,連接BE、DF,以B為原點建立平面直角坐標系,使BC、BA邊分別在x軸和y軸的正半軸上.

(1)試判斷四邊形BFDE的形狀,并說明理由;
(2)求直線EF的解析式.
【答案】(1)四邊形BFDE是菱形,見解析;(2)y=﹣2x+10.
【解析】
(1)根據矩形的性質及等腰三角形的特點即可求出四邊 相等,故可求解;
(2)設AE=x,得BE=DE=8﹣x,利用在Rt△ABE中利用勾股定理求出x,得到E點和點F的坐標,再根據待定系數法確定函數關系式進行求解.
解:(1)四邊形BFDE是菱形,理由如下:
由題意可知:DE=BE,DF=BF,∠DEF=∠BEF,
∵四邊形ABCD是矩形,
∴AD∥BC,
∴∠DEF=∠BFE,
∴∠BEF=∠BFE,
∴BE=BF,
∴BE=BF=DF=DE,
∴四邊形BFDE是菱形;
(2)設AE=x,
∵AD=8,AB=4,
∴BE=DE=8﹣x,
在Rt△ABE中,∠BAE=90°,
∴AB2+AE2=BE2,
∴42+x2=(8﹣x)2,
解得:x=3,
∴AE=3,BF=5,
∴E點的坐標是(3,4),點F的坐標是(5,0),
設直線EF的解析式為y=kx+b,
可得方程組![]() ,
,
解這個方程組得![]() ,
,
∴直線EF的解析式是y=﹣2x+10.


科目:初中數學 來源: 題型:
【題目】有兩張完全重合的矩形紙片,小亮同學將其中一張繞點A順時針旋轉90°后得到矩形AMEF(如圖1),連接BD、MF,若此時他測得BD=8cm,∠ADB=30度.請回答下列問題:(1)試探究線段BD與線段MF的關系,并簡要說明理由;
(2)小紅同學用剪刀將△BCD與△MEF剪去,與小亮同學繼續探究.他們將△ABD繞點A順時針旋轉得△AB1D1,AD1交FM于點K(如圖2),設旋轉角為β(0°<β<90°),當△AFK為等腰三角形時,請直接寫出旋轉角β的度數;
(3)若將△AFM沿AB方向平移得到△A2F2M2(如圖3),F2M2與AD交于點P,A2M2與BD交于點N,當NP∥AB時,求平移的距離是多少?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我國男性的體質系數計算公式是:m=![]() ×100%,其中W表示體重(單位:kg),H表示身高(單位:cm).通過計算出的體質系數m對體質進行評價.具體評價如下表:
×100%,其中W表示體重(單位:kg),H表示身高(單位:cm).通過計算出的體質系數m對體質進行評價.具體評價如下表:
m | <80% | 80%~90% | 90%~110% | 110%~120% | >120% |
評價結果 | 明顯消瘦 | 消瘦 | 正常 | 過重 | 肥胖 |
(1)某男生的身高是170cm,體重是75kg,他的體質評價結果是 ;
(2)現從某校九年級學生中隨機抽取n名男生進行體質評價,評價結果統計如下:
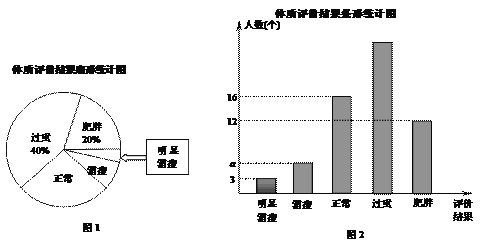
①抽查的學生數n= ;圖2中a的值為 ;
②圖1中,體質評價結果為“正常”的所在扇形圓心角為 °;
(3)若該校九年級共有男生480人,試估計該校九年級體質評價結果為“過重”或“肥胖”的男生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
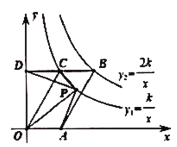
【題目】如圖,□![]() 的頂點
的頂點![]() 的坐標為
的坐標為![]() ,
,![]() 在第一象限反比例函數
在第一象限反比例函數![]() 和
和![]() 的圖象分別經過
的圖象分別經過![]() 兩點,延長
兩點,延長![]() 交
交![]() 軸于點
軸于點![]() . 設
. 設![]() 是反比例函數
是反比例函數![]() 圖象上的動點,若
圖象上的動點,若![]() 的面積是
的面積是![]() 面積的2倍,
面積的2倍,![]() 的面積等于
的面積等于![]() ,則
,則![]() 的值為________。
的值為________。
查看答案和解析>>
科目:初中數學 來源: 題型:
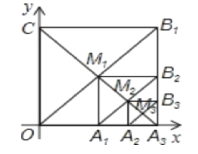
【題目】如圖,在平面直角坐標系中,邊長為1的正方形OA1B1C的對角線A1C和OB1交于點M1;以M1A1為對角線作第二個正方形A2A1B2M,對角線A1M1和A2B2交于點M2;以M2A1為對角線作第三個正方形A3A1B3M2,對角線A1M2和A3B3交于點M3;..依此類推,這樣作的第6個正方形對角線交點的坐標為____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】老師在黑板上出了一道解方程的題:4(2x﹣1)=1﹣3(x+2),小明馬上舉手,要求到黑板上做,他是這樣做的:8x﹣4=1﹣3x+6,①
8x﹣3x=1+6﹣4,②
5x=3,③
x=![]() .④
.④
老師說:小明解一元一次方程沒有掌握好,因此解題時出現了錯誤,請你指出他錯在哪一步:________(填編號),并說明理由.然后,你自己細心地解這個方程.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了了解學生對語文、數學、英語、物理四科的喜愛程度(每人只選一科),特對八年級某班進行了調查,并繪制成如下頻數和頻率統計表和扇形統計圖:
科目 | 頻數 | 頻率 |
語文 |
| 0.5 |
數學 | 12 |
|
英語 | 6 |
|
物理 |
| 0.2 |

(1)求出這次調查的總人數;
(2)求出表中![]() 的值;
的值;
(3)若該校八年級有學生1000人,請你算出喜愛英語的人數,并發表你的看法.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,∠C=90°,AC=12,BC=9,AB=15,若動點P從點C開始,按C→A→B→C的路徑運動,且速度為每秒3個單位,設運動的時間為t秒.
(1)當t=______時,CP把△ABC的面積分成相等的兩部分;
(2)當t=5時,CP把△ABC分成的兩部分面積之比是S△APC:S△BPC=______
(3)當t=______時,△BPC的面積為18.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com