
【題目】在Rt△ABC中,∠ABC=90°,AB=BC,E、M分別為AB、AC上的點,連接CE,BM交于點G,且BM⊥CE,O為AC的中點,連接BO交CE于點N.
(1)如圖①,若AB=6,2MO=AM,求BM的長;
(2)如圖②,連接OG、AG,若AG⊥OG,求證:AC=![]() BG.
BG.

【答案】(1)2![]() ;(2)詳見解析.
;(2)詳見解析.
【解析】
(1)由等腰三角形底邊中線是底邊的高可知OB⊥AC,根據(jù)等腰直角三角形可求出OB=OC=OA=3![]() ,根據(jù)2MO=AM即可求出OM的長,根據(jù)勾股定理求出BM的長即可.(2)過O作OF//AG交CG于F,則∠COF=∠OGA=90°,即可證明∠COF=∠GOB,由O是AC中點可知CF=FG,通過證明△COF≌△OBG即可證明CF=GF=BG,根據(jù)勾股定理可求出AC=
,根據(jù)2MO=AM即可求出OM的長,根據(jù)勾股定理求出BM的長即可.(2)過O作OF//AG交CG于F,則∠COF=∠OGA=90°,即可證明∠COF=∠GOB,由O是AC中點可知CF=FG,通過證明△COF≌△OBG即可證明CF=GF=BG,根據(jù)勾股定理可求出AC=![]() BG.
BG.
(1)∵OB是Rt△ABC斜邊中線,
∴OB=OC=OA,
∵AB=BC=6,
∴OB⊥BC,AC=![]() =6
=6![]() ,
,
∴OB=OA=3![]() ,
,
∵2MO=AM,
∴OM=![]() ,
,
∴BM=![]() =2
=2![]() ,
,
(2)過點O作OF//AG交CG于F,
∵OF//AG,O為AC中點,AG⊥OG
∴CF=FG,∠FOG=∠AOG=90°,
∵∠COF+∠FOB=90°,∠GOB+∠FOB=90°,
∴∠COF=∠GOB,
∵∠OCF+∠CON=90°,∠OBG++∠BNG=90°,∠CON=∠BNG,
∴∠OCF=∠OBG,
在△OCF和△OBG中,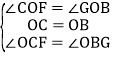
∴△OCF≌△OBG,
∴BG=CF=FG,
在Rt△CBG中,BC=![]() =
=![]() BG,
BG,
在Rt△ABC中,AC=![]() BC=
BC=![]() BG.
BG.


科目:初中數(shù)學 來源: 題型:
【題目】如圖,在△ABC中,AB=CB,∠ABC=90°,D為AB延長線上一點,點E在BC邊上,且BE=BD,連結AE、DE、DC

①求證:△ABE≌△CBD;
②若∠CAE=30°,求∠BDC的度數(shù).
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在水上治安指揮塔![]() 西側兩條航線
西側兩條航線![]() 、
、![]() 上有兩艘巡邏艇
上有兩艘巡邏艇![]() 與
與![]() 所在航線靠近
所在航線靠近![]() ,直線
,直線![]() 、
、![]() 間的距離
間的距離![]() ,點
,點![]() 在點
在點![]() 的南偏西
的南偏西![]() 方向上,且
方向上,且![]() ,
,![]() 在
在![]() 的北偏東
的北偏東![]() 方向上.求:
方向上.求:

![]() 巡邏艇
巡邏艇![]() 與塔
與塔![]() 之間的距離
之間的距離![]() .(結果保留根號)
.(結果保留根號)
![]() 已知巡邏艇
已知巡邏艇![]() 的速度每小時比巡邏艇
的速度每小時比巡邏艇![]() 快
快![]() ,當兩艘巡邏艇同時到達指揮塔
,當兩艘巡邏艇同時到達指揮塔![]() 的正南方向時,求巡邏艇
的正南方向時,求巡邏艇![]() 的速度.
的速度.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,![]() ,點
,點![]() 是
是![]() 邊上一點,點
邊上一點,點![]() ,
,![]() 是
是![]() 邊上兩點,且
邊上兩點,且![]() ,作點
,作點![]() 關于
關于![]() 的對稱點點
的對稱點點![]() ,連接
,連接![]() ,
,![]() ,
,![]() .
.

(1)依題意補全圖形;
(2)猜想![]() ______°,并證明;
______°,并證明;
(3)猜想線段![]() 、
、![]() 、
、![]() 的數(shù)量關系______,并證明.
的數(shù)量關系______,并證明.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】最近,“校園安全”受到全社會的廣泛關注,巫溪中學對部分學生就校園安全知識的了解程度, 采用隨機抽樣調查的方式,并根據(jù)收集到的信息進行統(tǒng)計,繪制了如下兩幅尚不完整的統(tǒng)計圖,請你根據(jù)統(tǒng)計圖中所提供的信息解答下列問題:
(1)扇形統(tǒng)計圖中“基本了解”部分對應扇形的圓心角為 度;請補全條形統(tǒng)計圖;
(2)若達到“了解”程度的人中有1名男生,2名女生,達到“不了解”程度的人中有1名男生和1名女生,若分別從達到“了解”程度和“不了解”程度的人中分別抽取1人參加校園知識競賽,請用樹狀圖或列表法求出恰好抽到1名男生和1名女生的概率.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,一次函數(shù)y=﹣x+7的圖象與正比例函數(shù)y=![]() x的圖象交于點A,點P(t,0)是x正半軸上的一個動點.
x的圖象交于點A,點P(t,0)是x正半軸上的一個動點.
(1)點A的坐標為( , );
(2)如圖1,連接PA,若△AOP是等腰三角形,求點P的坐標:
(3)如圖2,過點P作x軸的垂線,分別交y=![]() x和y=﹣x+7的圖象于點B,C.是否存在正實數(shù),使得BC=
x和y=﹣x+7的圖象于點B,C.是否存在正實數(shù),使得BC=![]() OA,若存在求出t的值;若不存在,請說明理由.
OA,若存在求出t的值;若不存在,請說明理由.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】今年黃金價格一路走高,![]() 月份的黃金價格比
月份的黃金價格比![]() 月份增長了
月份增長了![]() ,由于受國際金價的影響,預計
,由于受國際金價的影響,預計![]() 月份的黃金價格比
月份的黃金價格比![]() 月份增長
月份增長![]() ,若這兩月黃金價格的平均增長率為
,若這兩月黃金價格的平均增長率為![]() ,則
,則![]() 滿足的關系式為( )
滿足的關系式為( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某汽車銷售公司經銷某品牌A款汽車,隨著汽車的普及,其價格也在不斷下降.今年5月份A款汽車的售價比去年同期每輛降價2萬元.如果賣出相同數(shù)量的A款汽車,去年銷售額為100萬元,今年銷售額只有90萬元.
(1)今年5月份A款汽車每輛銷售多少萬元?
(2)為了增加收入,汽車銷售公司決定再經銷同品牌的B款汽車,已知A款汽車每輛進價為8.5萬元,B款汽車每輛進價為6萬元,公司預計用多于100萬元且少于110萬元的資金購進這兩款汽車共15輛,問有幾種進貨方案?
(3)在(2)的前提下,如果B款汽車每輛售價為12萬元,為打開B款汽車的銷路,公司決定每售出一輛B款汽車,獎勵顧客現(xiàn)金1.8萬元,怎樣進貨公司的利潤最大(假設能全部賣出)?最大利潤是多少?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,∠AOB=20°,點M,N分別是邊OA,OB上的定點,點P,Q分別是邊OB、OA上的動點,記∠MPQ=α,∠PQN=β,當MP+PQ+QN最小時,則β﹣α的值為_____.
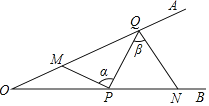
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com