
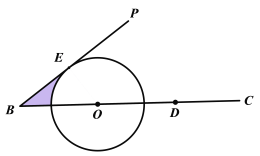
【題目】如圖,已知∠PBC,在射線BC上任取一點D,以線段BD的中點O為圓心作⊙O,且⊙O與PB相切于點E.
(1)求作:射線BP上一點A,使△ABD為等腰三角形,且AB=AD.(要求:運用直尺和圓規,保留作圖痕跡,不寫作法)
(2)求證:AD是⊙O的切線.
(3)若BD的長為8cm,∠PBC=30°,求陰影部分的面積
【答案】(1)見解析;(2)見解析;(3)![]() -
-![]() .
.
【解析】
(1)根據等腰三角形的性質,利用尺規作圖作出圖象即可;
(2)過點O作OF⊥AD,垂足為F,連接OE,根據△ABD為等腰三角形,點O是底邊BD的中點,可得出AO是∠BAD的角平分線,可得OE=OF,即可得證;
(3)根據已知條件可推出∠EOB=60°,BE=![]() =
=![]() ,再根據S陰影=S△BOE-S扇形EOM即可得解.
,再根據S陰影=S△BOE-S扇形EOM即可得解.
(1)作圖如下,
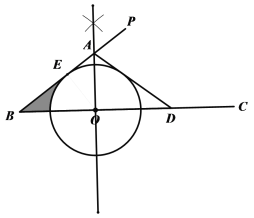
(2)證明:如圖,過點O作OF⊥AD,垂足為F,連接OE,
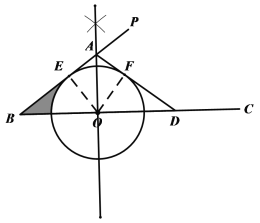
∵⊙O與PB相切于點E,
∴OE⊥AB,
∵△ABD為等腰三角形,點O是底邊BD的中點,
∴AO是∠BAD的角平分線,
∴OE=OF,即OF是⊙O的半徑,
∴AC與⊙O相切;
(3)解:由(2)知,∠BEO=90°,
∵∠PBC=30°,
∴∠EOB=60°,
∵BD的長為8cm且點O是底邊BD的中點,
∴OB=OD=![]() BD=
BD=![]() ×8=4cm,
×8=4cm,
∴OE=![]() OB=2cm,
OB=2cm,
在Rt△BOE中,根據勾股定理得BE=![]() =
=![]() ,
,
∴S陰影=S△BOE-S扇形EOM=![]() ×
×![]() ×2-
×2-![]() =
=![]() -
-![]() .
.


科目:初中數學 來源: 題型:
【題目】借鑒我們已有的研究函數的經驗,探索函數y=|x2﹣2x﹣3|﹣2圖象和性質,探究過程如下,請補充完整.
(1)自變量x的取值范圍是全體實數,x與y的幾組對應值列表如下:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 10 | m | ﹣2 | 1 | n | 1 | ﹣2 | 3 | 10 | … |
其中,m= ,n= ;
(2)根據上表數據,在如圖所示的平面直角坐標系中描點,并畫出函數圖象;
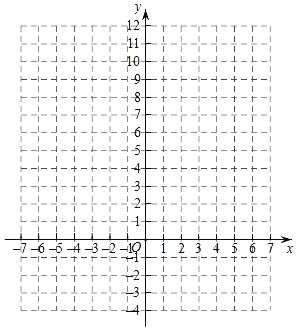
(3)觀察函數圖象:
①當方程|x2﹣2x﹣3|=b+2有且僅有兩個不相等的實數根時,根據函數圖象直接寫出b的取值范圍為 .
②在該平面直角坐標系中畫出直線y=![]() x+2的圖象,根據圖象直接寫出該直線與函數y=|x2﹣2x﹣3|﹣2的交點橫坐標為: (結果保留一位小數).
x+2的圖象,根據圖象直接寫出該直線與函數y=|x2﹣2x﹣3|﹣2的交點橫坐標為: (結果保留一位小數).
查看答案和解析>>
科目:初中數學 來源: 題型:
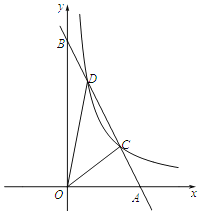
【題目】如圖,已知直線y=﹣2x+4與x軸交于點A,與y軸交于點B,與雙曲線y=![]() (x>0)交于C、D兩點,且∠AOC=∠ADO,則k的值為_____.
(x>0)交于C、D兩點,且∠AOC=∠ADO,則k的值為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有![]() 兩個黑布袋,
兩個黑布袋,![]() 布袋中有四個除標號外完全相同的小球,小球上分別標有數字
布袋中有四個除標號外完全相同的小球,小球上分別標有數字![]() 布袋中有三個除標號外完全相同的小球,小球上分別標有數字
布袋中有三個除標號外完全相同的小球,小球上分別標有數字![]() 小明先從
小明先從![]() 布袋中隨機取出一個小球,用
布袋中隨機取出一個小球,用![]() 表示取出的球上標有的數字,再從
表示取出的球上標有的數字,再從![]() 布袋中隨機取出一個小球,用
布袋中隨機取出一個小球,用![]() 來表示取出的球上標有的數字.
來表示取出的球上標有的數字.
(1)若用![]() 表示小明取球時
表示小明取球時![]() 與
與![]() 的對應值,請畫出樹狀圖,并寫出
的對應值,請畫出樹狀圖,并寫出![]() 的所有取值;
的所有取值;
(2)求關于![]() 的一元二次方程
的一元二次方程![]() 有實數根的概率.
有實數根的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
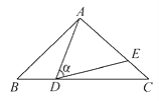
【題目】如圖,在△ABC中,AB=AC=10,點D是邊BC上一動點(不與B,C重合),∠ADE=∠B=α,DE交AC于點E,且cosα=![]() .下列結論:①△ADE∽△ACD;②當BD=6時,△ABD與△DCE全等;③△DCE為直角三角形時,BD為8;④0<CE≤6.4.其中正確的結論是________.(把你認為正確結論的序號都填上)
.下列結論:①△ADE∽△ACD;②當BD=6時,△ABD與△DCE全等;③△DCE為直角三角形時,BD為8;④0<CE≤6.4.其中正確的結論是________.(把你認為正確結論的序號都填上)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在Rt△ACB和Rt△AEF中,∠ACB=∠AEF=90°,若點P是BF的中點,連接PC,PE.
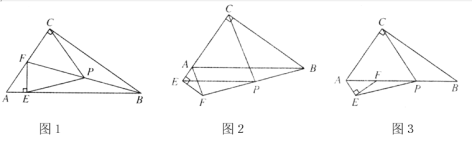
(1) 如圖1,若點E,F分別落在邊AB,AC上,求證:PC=PE;
(2) 如圖2,把圖1中的△AEF繞著點A順時針旋轉,當點E落在邊CA的延長線上時,探索PC與PE的數量關系,并說明理由.
(3) 如圖3,把圖2中的△AEF繞著點A順時針旋轉,點F落在邊AB上.其他條件不變,問題(2)中的結論是否發生變化?如果不變,請加以證明;如果變化,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知A、B兩點的坐標分別為(―2,0),(0,1),⊙C的圓心坐標為(0,―1),半徑為1.若D是⊙C上的一個動點,射線AD與y軸交于點E,則△ABE面積的最大值是( ) 
A. 4 B. ![]() C.
C. ![]() D. 3
D. 3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com