
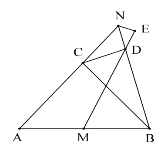
【題目】如圖,△ABC 為等腰直角三角形,∠ACB=90°,點 M 為 AB 邊的中點,點 N 為射線 AC 上一點,連接 BN,過點 C 作 CD⊥BN 于點 D,連接 MD,作∠BNE=∠BNA,邊 EN 交射線 MD 于點 E,若 AB=20![]() ,MD=14
,MD=14![]() ,則 NE 的長為___.
,則 NE 的長為___.
【答案】![]()
【解析】
連接CM,過點M作MF⊥BD于F,根據等腰直角三角形的性質求出BM、BC,證出C、M、B、D四點共圓,根據圓周角定理的推論和等腰三角形的判定證出△DMF為等腰直角三角形,利用勾股定理和銳角三角函數求出BD和BN,然后證出△NDE∽△MDB列出比例式即可求出結論.
解:連接CM,過點M作MF⊥BD于F

∵△ABC 為等腰直角三角形,∠ACB=90°,點 M 為 AB 邊的中點,AB=20![]() ,
,
∴BM=![]() AB=10
AB=10![]() ,AC=BC=20,∠CMB=90°,∠BCM=
,AC=BC=20,∠CMB=90°,∠BCM=![]() ∠ACB=45°
∠ACB=45°
∵CD⊥BN
∴∠CDB=90°
∴∠CDB+∠CMB=180°
∴C、M、B、D四點共圓
∴∠MDB=∠BCM=45°,∠DCB=∠BMD
∴△DMF為等腰直角三角形
∵MD=14![]() ,
,
∴MF=DF=14
在Rt△BMF中,BF=![]()
∴BD=BF+DF=16
∵cos∠CBN=![]()
即![]()
解得:BN=25
∴DN=BN-BD=9
∵∠BNE=∠BNA,而∠DCN+∠BNA=90°
∴∠BNE+∠DCN=90°
∵∠DCN+∠DCB=90°
∴∠BNE=∠DCB
∴∠BNE=∠BMD
∵∠NDE=∠MDB
∴△NDE∽△MDB
∴![]()
即![]()
解得:NE=![]()
故答案為:![]() .
.


 寒假天地重慶出版社系列答案
寒假天地重慶出版社系列答案科目:初中數學 來源: 題型:
【題目】有兩張完全重合的矩形紙片,將其中一張繞點![]() 順時針旋轉
順時針旋轉![]() 后得到矩形
后得到矩形![]() (如圖1),連接
(如圖1),連接![]() ,
,![]() ,若
,若![]() ,
,![]() .
.

(1)試探究線段![]() 與線段
與線段![]() 的數量關系和位置關系,并說明理由;
的數量關系和位置關系,并說明理由;
(2)把![]() 與
與![]() 剪去,將
剪去,將![]() 繞點
繞點![]() 順時針旋轉得
順時針旋轉得![]() ,邊
,邊![]() 交
交![]() 于點
于點![]() (如圖2),設旋轉角為
(如圖2),設旋轉角為![]() ,當
,當![]() 為等腰三角形時,求
為等腰三角形時,求![]() 的度數;
的度數;
(3)若將![]() 沿
沿![]() 方向平移得到
方向平移得到![]() (如圖3),
(如圖3),![]() 與
與![]() 交于點
交于點![]() ,
,![]() 與
與![]() 交于點
交于點![]() ,當
,當![]() 時,求平移的距離.
時,求平移的距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】關于二次函數![]() ,以下結論:①拋物線交
,以下結論:①拋物線交![]() 軸有兩個不同的交點;②不論
軸有兩個不同的交點;②不論![]() 取何值,拋物線總是經過一個定點;③設拋物線交
取何值,拋物線總是經過一個定點;③設拋物線交![]() 軸于
軸于![]() 、
、![]() 兩點,若
兩點,若![]() ,則
,則![]() ;④拋物線的頂點在
;④拋物線的頂點在![]() 圖象上;⑤拋物線交
圖象上;⑤拋物線交![]() 軸于
軸于![]() 點,若
點,若![]() 是等腰三角形,則
是等腰三角形,則![]() ,
,![]() ,
,![]() .其中正確的序號是( )
.其中正確的序號是( )
A. ①②⑤ B. ②③④ C. ①④⑤ D. ②④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校隨機對本校部分學生進行“假期中,我在家可以這么做:![]() .扎實學習、
.扎實學習、![]() .快樂游戲、
.快樂游戲、![]() .經典閱讀、
.經典閱讀、![]() .分擔勞動、
.分擔勞動、![]() .樂享健康”網絡調查,并根據調查結果繪制成如下兩幅不完整的統計圖(若每一位同學只能選擇一項),請根據圖中信息,回答下列問題.
.樂享健康”網絡調查,并根據調查結果繪制成如下兩幅不完整的統計圖(若每一位同學只能選擇一項),請根據圖中信息,回答下列問題.

(1)這次調查的總人數是___________人;
(2)請補全條形統計圖,并說明扇形統計圖中![]() 所對應的圓心角是___________度;
所對應的圓心角是___________度;
(3)若該學校共有學生1700人,則選擇![]() 有多少人?
有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,弦CD與AB相交,連接CO,過點D作⊙O的切線,與AB的延長線交于點E,若DE∥AC,∠BAC=40°,則∠OCD的度數為( )
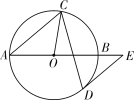
A.65°B.30°C.25°D.20°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為推動陽光體育運動的廣泛開展,引導學生走向大自然,走到陽光下積極參加體育鍛煉,學校準備購買一批運動鞋供學生借用,現從各年級隨機抽取了部分學生的鞋號,繪制了如圖所示兩個統計圖,請根據相關信息,解答下列問題:
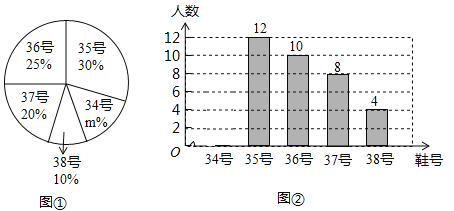
(1)求本次抽樣調查的學生人數
(2)通過計算補全條形統計圖和扇形統計圖;
(3)若學生計劃購買200雙運動鞋,建議購買35號運動鞋約多少雙?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com