
【題目】在![]() 中,
中,![]() ,
,![]() ,點
,點![]() 是
是![]() 上一點.
上一點.
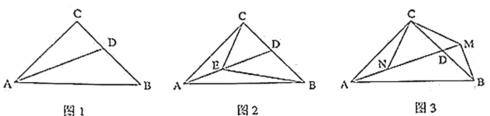
(1)如圖![]() ,
,![]() 平分
平分![]() .求證:
.求證:![]() ;
;
(2)如圖![]() ,點
,點![]() 在線段
在線段![]() 上,且
上,且![]() ,
,![]() ,求證:
,求證:![]() .
.
(3)如圖![]() ,
,![]() ,過
,過![]() 點作
點作![]() 交
交![]() 的延長線于點
的延長線于點![]() ,連接
,連接![]() ,過
,過![]() 點作
點作![]() 交
交![]() 于
于![]() ,求證:
,求證:![]() .
.
【答案】(1)見解析;(2)見解析;(3)見解析
【解析】
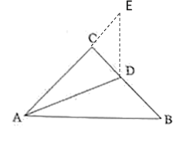
(1)延長AC至E,使CE=CD,利用AAS證出△BAD≌△EAD,從而得出AB=AE,即可證出結論;
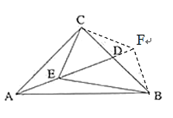
(2)過點C作CF⊥EC交AD的延長線于點F,連接BF,先利用SAS證出△ACE≌△BCF,從而證出AE=BF,∠CEA=∠CFB,再證出∠EFB=90°,利用30°所對的直角邊是斜邊的一半即可證出結論;
(3)過點C作CE⊥AM于M,先利用AAS證出△CNA≌△CMB,即可證出CN=CM,根據等腰三角形的性質可得NE=EM,然后利用AAS證出△CED≌△BMD,從而得出ED=DM,然后根據線段的關系即可得出結論.
解:(1)延長AC至E,使CE=CD
∵![]() ,
,![]()
∴∠ECD=180°-∠ACB=90°,∠B=∠CAB=![]() (180°-∠ACB)=45°
(180°-∠ACB)=45°
∴△CDE為等腰三角形
∴∠E=45°
∴∠B=∠E
∵![]() 平分
平分![]()
∴∠BAD=∠EAD
在△BAD和△EAD中
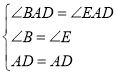
∴△BAD≌△EAD
∴AB=AE
∵AE=AC+CE=AC+CD
∴AB= AC+CD
(2)過點C作CF⊥EC交AD的延長線于點F,連接BF
∵∠CED=45°
∴△CEF為等腰直角三角形
∴CE=CF,∠CFE=∠CEF=45°
∵△ABC為等腰直角三角形
∴∠ACB=90°,CA=CB,
∴∠ACE+∠ECB=90°,∠BCF+∠ECB=90°
∴∠ACE=∠BCF
在△ACE和△BCF中
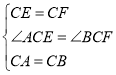
∴△ACE≌△BCF
∴AE=BF,∠CEA=∠CFB
∵∠CEA=180°-∠CEF=135°
∴∠CFB=135°
∴∠EFB=∠CFB-∠CFE=90°
在Rt△EFB中,∠BEF=30°
∴BE=2BF
∴BE=2AE
(3)過點C作CE⊥AM于M,
∵△ABC為等腰直角三角形
∴∠ACB=90°,CA=CB
∵CN⊥CM,BM⊥AM
∴∠NCM=90°,∠BMA=90°
∴∠ACN+∠NCB=90°,∠BCM+∠NCB=90°,
∴∠ACN=∠BCM
∴∠CNA=∠NCM+∠CMN=90°+∠CMN=∠CMB
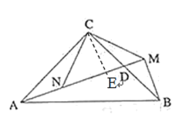
在△CNA和△CMB中
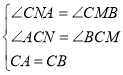
∴△CNA≌△CMB
∴CN=CM
∴△CNM為等腰直角三角形
∴NE=EM
在△CED和△BMD中
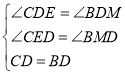
∴△CED≌△BMD
∴ED=DM
∴EM=2DM
∴NE=2DM
∴DN=NE+ED=3DM


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】(8分)如圖,已知O是坐標原點,B、C兩點的坐標分別為(3,-1)、(2,1)。

(1)以O點為位似中心在y軸的左側將△OBC放大到兩倍畫出圖形。
(2)寫出B、C兩點的對應點B、C的坐標;
(3)如果△OBC內部一點M的坐標為(x,y),寫出M的對應點M的坐標。
查看答案和解析>>
科目:初中數學 來源: 題型:
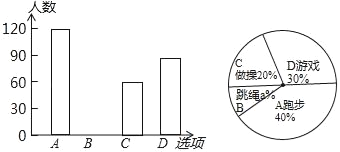
【題目】某校在一次大課間活動中,采用了四鐘活動形式:A、跑步,B、跳繩,C、做操,D、游戲.全校學生都選擇了一種形式參與活動,小杰對同學們選用的活動形式進行了隨機抽樣調查,根據調查統計結果,繪制了不完整的統計圖.
請結合統計圖,回答下列問題:
(1)這次調查中,一共調查了多少名學生?
(2)求出扇形統計圖中“B:跳繩”所對扇形的圓心角的度數,并補全條形圖;
(3)若該校有2000名學生,請估計選擇“A:跑步”的學生約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
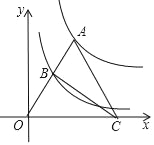
【題目】如圖,點A為函數y=![]() (x>0)圖象上一點,連結OA,交函數y=
(x>0)圖象上一點,連結OA,交函數y=![]() (x>0)的圖象于點B,點C是x軸上一點,且AO=AC,則△OBC的面積為____.
(x>0)的圖象于點B,點C是x軸上一點,且AO=AC,則△OBC的面積為____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】兩個工程隊共同參與一項筑路工程,若先由甲、乙兩隊合作![]() 天,剩下的工程再由乙隊單獨做
天,剩下的工程再由乙隊單獨做![]() 天可以完成,共需施工費
天可以完成,共需施工費![]() 萬元;若由甲、乙合作完成此項工程共需
萬元;若由甲、乙合作完成此項工程共需![]() 天,共需施工費
天,共需施工費![]() 萬元.
萬元.
(1)求乙隊單獨完成這項工程需多少天?
(2)甲、乙兩隊每天的施工費各為多少萬元?
(3)若工程預算的總費用不超過![]() 萬元,則乙隊最少施工多少天?
萬元,則乙隊最少施工多少天?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,D、E分別是AC、AB上的點,BD與CE相交于點O,給出四個條件:①OB=OC;②∠EBO=∠DCO;③∠BEO=∠CDO;④BE=CD.上述四個條件中,選擇兩個可以判定△ABC是等腰三角形的方法有( )
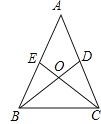
A.2種B.3種C.4種D.6種
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某文具店銷售A、B兩種文具,其中A文具的定價為20元/件,B產品的定價10元/件.
(1)若該文具按定價售出A、B兩種文具共400件,若銷售總額不低于5000元,則至少銷售A產品多少件?
(2)該文具店2018年2月按定價銷售A文具280件,B文具120件,2018年3月,市場情況發生變化,A文具銷售價與上個月持平,但這個月的銷售量比上個月減少了m%;B文具的銷售價比上個月減少了m%,但銷售量增加了![]() m%;3月份的銷售總金額與2月份保持不變.求m的值.
m%;3月份的銷售總金額與2月份保持不變.求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖(a)所示點D是等邊![]() 邊BA上一動點(點D與點B不重合),連接DC,以DC為邊在BC上方作等邊
邊BA上一動點(點D與點B不重合),連接DC,以DC為邊在BC上方作等邊![]() ,連接AF.你能發現線段AF與BD之間的數量關系嗎?并證明.
,連接AF.你能發現線段AF與BD之間的數量關系嗎?并證明.
(2)如圖(b)所示當動點D運動至等邊![]() 邊BA的延長線上時,其他作法與(1)相同,猜想AF與BD在(1)中的結論是否仍然成立?(直接寫出結論)
邊BA的延長線上時,其他作法與(1)相同,猜想AF與BD在(1)中的結論是否仍然成立?(直接寫出結論)
(3)①如圖(c)所示,當動點D在等邊![]() 邊BA上運動時(點D與點B不重合),連接DC,以DC為邊在BC上方、下方分別作等邊
邊BA上運動時(點D與點B不重合),連接DC,以DC為邊在BC上方、下方分別作等邊![]() 和等邊
和等邊![]() ,連接AF、
,連接AF、![]() ,探究AF、
,探究AF、![]() 與AB有何數量關系?并證明.
與AB有何數量關系?并證明.
②如圖(d)所示,當動點D在等邊![]() 邊BA的延長線上運動時,其他作法與(3)①相同,①中的結論是否成立?若不成立,是否有新的結論?并證明.
邊BA的延長線上運動時,其他作法與(3)①相同,①中的結論是否成立?若不成立,是否有新的結論?并證明.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在梯形ABCD中,∠ABC=90,AE∥CD交BC于E,O是AC的中點,AB=![]() ,AD=2,BC=3,下列結論:
,AD=2,BC=3,下列結論:
①∠CAE=30;②AC=2AB;③S△ADC=2S△ABE;④BO⊥CD,其中正確的是()

A. ①②③ B. ②③④ C. ①③④ D. ①②③④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com