
【題目】如圖,在矩形ABCD中,點E,F分別是BC,DC上的一個動點,以EF為對稱軸折疊△CEF,使點C的對稱點G落在AD上,若AB=3,BC=5,則CF的取值范圍為 . 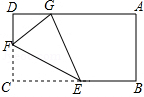
【答案】![]() ≤CF≤3
≤CF≤3
【解析】解:∵四邊形ABCD是矩形, ∴∠C=90°,BC=AD=5,CD=AB=3,
當點D與F重合時,CF最大=3,如圖1所示: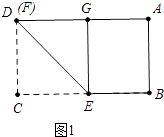
當B與E重合時,CF最小,如圖2所示:
在RTABG中,∵BG=BC=5,AB=3,
∴AG= ![]() =4,
=4,
∴DG=AD﹣AG=1,設CF=FG=x,
在RT△DFG中,∵DF2+DG2=FG2 ,
∴(3﹣x)2+12=x2 ,
∴x= ![]() ,
,
∴ ![]() ≤CF≤3.
≤CF≤3.
故答案為 ![]() ≤CF≤3.
≤CF≤3.
當點E與B重合時,CF最小,先利用勾股定理求出AG,設CF=FG=x,在RT△DFG中,利用勾股定理列出方程即可解決問題,.當F與D重合時,CF最大.由此即可解決問題.


科目:初中數學 來源: 題型:
【題目】如圖,在邊長為1個單位長度的小正方形組成的網格中,給出了格點三角形ABC(頂點是網格線的交點)
(1)先將△ABC豎直向上平移5個單位,再水平向右平移4個單位得到△A1B1C1,請畫出△A1B1C1;
(2)將△A1B1C1繞B1點順時針旋轉90°,得△A2B1C2,請畫出△A2B1C2;
(3)求線段B1C1變換到B1C2的過程中掃過區域的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,則下列結論:①DE=CD;②AD平分∠CDE;③∠BAC=∠BDE;④BE+AC=AB,其中正確的是( )

A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形OABC中,已知點A、C兩點的坐標為A (![]() ,
,![]() ),C (2
),C (2![]() ,0).
,0).
(1)求點B的坐標.
(2)將平行四邊形OABC向左平移![]() 個單位長度,求所得四邊形A′B′C′O′四個頂點的坐標.
個單位長度,求所得四邊形A′B′C′O′四個頂點的坐標.
(3)求平行四邊形OABC的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為加快城市群的建設與發展,在A,B兩城市間新建一條城際鐵路,建成后,鐵路運行里程由現在的120km縮短至114km,城際鐵路的設計平均時速要比現行的平均時速快110km,運行時間僅是現行時間的![]() ,求建成后的城際鐵路在A,B兩地的運行時間.
,求建成后的城際鐵路在A,B兩地的運行時間.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一樓房AB后有一假山,其坡度為i=1: ![]() ,山坡坡面上E點處有一休息亭,測得假山坡腳C與樓房水平距離BC=25米,與亭子距離CE=20米,小麗從樓房頂測得E點的俯角為45°,求樓房AB的高.(注:坡度i是指坡面的鉛直高度與水平寬度的比)
,山坡坡面上E點處有一休息亭,測得假山坡腳C與樓房水平距離BC=25米,與亭子距離CE=20米,小麗從樓房頂測得E點的俯角為45°,求樓房AB的高.(注:坡度i是指坡面的鉛直高度與水平寬度的比)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=﹣x2+bx+c與x軸相交于A、B兩點,與y軸相交于點C,且點B與點C的坐標分別為B(3,0).C(0,3),點M是拋物線的頂點.
(1)求二次函數的關系式;
(2)點P為線段MB上一個動點,過點P作PD⊥x軸于點D.若OD=m,△PCD的面積為S,試判斷S有最大值或最小值?并說明理由;
(3)在MB上是否存在點P,使△PCD為直角三角形?如果存在,請直接寫出點P的坐標;如果不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知MB=ND,∠MBA=∠NDC,下列條件中不能判定△ABM≌△CDN的是( )

A. ∠M=∠N B. AM=CN C. AB=CD D. AM∥CN
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com