【題目】如圖，在平面直角坐標系xOy中，一次函數
的圖象與正比例函數
的圖象交于點A（m，4）．
（1）求m、n的值；
（2）設一次函數的圖象與x軸交于點B，求△AOB的面積；
（3）直接寫出使函數的值小于函數的值的自變量x的取值范圍．
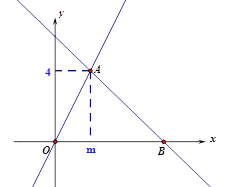
【答案】（1）m=2,n=6;(2)12;(3)x>2.
【解析】試題（1）先把A（m，4）代入正比例函數解析式可計算出m=2，然后把A（2，4）代入y=-x+n計算出n的值；
（2）先確定B點坐標，然后根據三角形面積公式計算；
（3）觀察函數圖象得到當x>2時，直線y=-x+n都在y=2x的下方，即函數y=－x+n的值小于函數y=2x的值．
試題解析：
（1）正比例函數
的圖象過點A（m，4）．
∴ 4=2 m，
∴ m =2 ．
又∵一次函數
的圖象過點A（m，4）．
∴ 4=-2+ n，
∴ n =6．
（2）一次函數的圖象與x軸交于點B，
∴令y=0，
∴x=6 點B坐標為（6,0）．
∴△AOB的面積
．
（3）∵由圖象得當x>2時，直線y=-x+n都在y=2x的下方
∴當x>2時，函數y=－x+n的值小于函數y=2x的值.
走進文言文系列答案科目：初中數學 來源： 題型：
【題目】（1）閱讀理解：
如圖①，在△ABC中，若AB=10，AC=6，求BC邊上的中線AD的取值范圍．
解決此問題可以用如下方法：延長AD到點E使DE=AD，再連接BE（或將△ACD繞著點D逆時針旋轉180°得到△EBD），把AB、AC，2AD集中在△ABE中，利用三角形三邊的關系即可判斷．
中線AD的取值范圍是 ；
（2）問題解決：
如圖②，在△ABC中，D是BC邊上的中點，DE⊥DF于點D，DE交AB于點E，DF交AC于點F，連接EF，求證：BE+CF＞EF；
（3）問題拓展：
如圖③，在四邊形ABCD中，∠B+∠D=180°，CB=CD，∠BCD=140°，以為頂點作一個70°角，角的兩邊分別交AB，AD于E、F兩點，連接EF，探索線段BE，DF，EF之間的數量關系，并加以證明．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀下面材料：如圖，點A、B在數軸上分別表示有理數a、b，則A、B兩點之間的距離可以表示為|a﹣b|.
根據閱讀材料與你的理解回答下列問題：
(1)數軸上表示3與﹣2的兩點之間的距離是 .
(2)數軸上有理數x與有理數7所對應兩點之間的距離用絕對值符號可以表示為 .
(3)代數式|x+8|可以表示數軸上有理數x與有理數 所對應的兩點之間的距離；若|x+8|=5，則x= .
(4)求代數式|x+1008|+|x+504|+|x﹣1007|的最小值.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小林同學積極參加體育鍛煉,天天堅持跑步,他每天以1000m為標準,超過的記作正數,不足的記作負數.下表是一周內小明跑步情況的記錄(單位：m)：
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
跑步情況(m) | +420 | +460 | -100 | -210 | -330 | +200 | -240 |
(1)星期三小林跑了_____米
(2)小林在跑得最少的一天跑了______米?跑得最多的一天比最少的一天多跑了_____米?
(3)若小林跑步的平均速度為240米/分，求本周內小明用于跑步的時間.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：如圖，反比例函數
的圖象與一次函數
的圖象交于點
、點
.
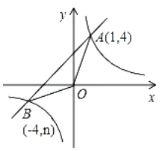
（1）求一次函數和反比例函數的解析式；
（2）求
的面積；
（3）直接寫出一次函數值大于反比例函數值的自變量
的取值范圍.
查看答案和解析>>
科目：初中數學 來源： 題型：
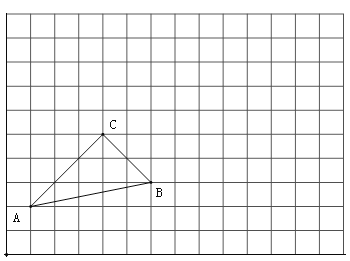
【題目】如圖，△ABC是格點三角形（各頂點是網格線的交點）， 每個小方格都是邊長為1個單位長度的小正方形．
（1）將△ABC向右平移6個單位長度，畫出平移后的△A1B1C1．
（2）將平移后的△A1B1C1繞點B1順時針旋轉90°，畫出旋轉后的△A2B1C2．
（3）將△ABC沿直線BC翻折，畫出翻折后的△A3BC.
（4）試問△ABC能否經過一次旋轉后與△A2B1C2重合，若能，請在圖中用字母O表示旋轉中心并寫出旋轉角的大小；若不能，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】探究：在數軸上描出下列各組數：1與3， 2與-5， -4與-1
（1） 觀察描在數軸上的每組數，說明表示每組數的兩點之間的距離與這組數有何關系？
答 ．
（2）若果a,b表示兩個有理數，判斷
____ 
（填＞，=或＜）
（3）當x為何值時：
與
的值相等。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知拋物線y=x2﹣2x+a（a＜0）與y軸相交于點A，頂點為M．直線y=
x﹣a分別與x軸，y軸相交于B，C兩點，并且與直線AM相交于點N．
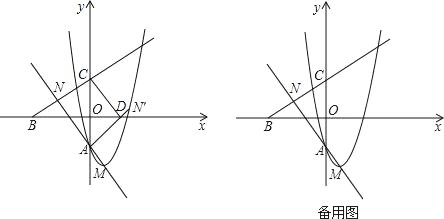
（1）試用含a的代數式分別表示點M與N的坐標；
（2）如圖，將△NAC沿y軸翻折，若點N的對應點N′恰好落在拋物線上，AN′與x軸交于點D，連接CD，求a的值和四邊形ADCN的面積；
（3）在拋物線y=x2﹣2x+a（a＜0）上是否存在一點P，使得以P，A，C，N為頂點的四邊形是平行四邊形？若存在，求出P點的坐標；若不存在，試說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某書店老板去圖書批發市場購買某種圖書，第一次用1200元購書若干本，并按該書定價7元出售，很快售完．由于該書暢銷，第二次購書時，每本書的批發價已比第一次提高了20%，他用1500元所購該書的數量比第一次多10本，當按定價售出200本時，出現滯銷，便以定價的4折售完剩余的書．
（1）第一次購書的進價是多少元？
（2）試問該老板這兩次售書總體上是賠錢了，還是賺錢了（不考慮其他因素）？若賠錢，賠多少；若賺錢，賺多少？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com