
【題目】如圖,在△ABC中,AB=AC=10,BC=16,點D是邊BC上(不與B,C重合)一動點,∠ADE=∠B,DE交AC于點E.
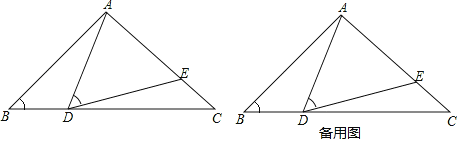
(1)求證:△ABD∽△DCE;
(2)若△DCE為直角三角形,求BD.
(3)若以AE為直徑的圓與邊BC相切,求AD;
【答案】(1)見解析;(2)BD=8或![]() ;(3)5
;(3)5![]()
【解析】
(1)證明∠ADB=∠DEC,即可得出結論;
(2)過點A作AG⊥BC于G,分兩種情況討論,當∠AED=90°時,當∠CDE=90°時通過三角形相似即可求得;
(3)取AE的中點O,過O作OF⊥BC于F,設BD=x,AE=y,可分別表示OA和OC,由OF∥AG,得出![]() ,得出關于x的方程,解出x即可求出DG長,則AD長可求出.
,得出關于x的方程,解出x即可求出DG長,則AD長可求出.
(1)證明:∵AB=AC,
∴∠B=∠C,
∵∠ADE=∠B,
∴∠ADE=∠C,
∵∠ADB=180°﹣∠ADE﹣∠CDE,∠DEC=180°﹣∠C﹣∠CDE,
∴∠ADB=∠DEC,
∵∠B=∠C,
∴△ABD∽△DCE;
(2)解:如圖1,過點A作AG⊥BC于G,

∴CG=![]() BC=8,
BC=8,
∴AG=![]() =6,
=6,
設∠ADE=∠B=∠C=α
∴cosα=![]() ,
,
當∠AED=90°時,
∵AB=AC,
∴∠B=∠C,
又∵∠ADE=∠B
∴∠ADE=∠C,
∴△ADE∽△ACD,
∵∠AED=90°,
∴∠ADC=90°,
即AD⊥BC,
∵AB=AC,
∴BD=CD,
∴BD=8.
當∠CDE=90°時,由(1)知△CDE∽△BAD,
∵∠CDE=90°,
∴∠BAD=90°,
∵cosα=![]() .AB=10,
.AB=10,
∴cosB=![]() ,
,
∴BD=![]() .
.
即:BD=8或![]() .
.
(3)解:如圖2,取AE的中點O,過O作OF⊥BC于F,

設BD=x,AE=y,
∴CD=BC﹣BD=16﹣x,CE=AC﹣AE=10﹣y,
由(1)知,△ABD∽△DCE,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴OA=![]() ,
,
∴OC=AC﹣OA
=10﹣![]()
![]() ,
,
∵以AE為直徑的圓與邊BC相切,
∴OF=OA=![]() ,
,
∵AG⊥BC,OF⊥BC,
∴OF∥AG,
∴![]() ,
,
∴OCAG=OFAC,
∴![]() ,
,
∴x=8+![]() 或x=8﹣
或x=8﹣![]() ,
,
∴DG=![]() ,
,
在Rt△AGD中,根據勾股定理得,AD=![]() =5
=5![]() .
.


 快樂5加2金卷系列答案
快樂5加2金卷系列答案科目:初中數學 來源: 題型:
【題目】已知函數![]() ,其中
,其中![]() 與
與![]() 成反比例
成反比例![]() 與
與![]() 成正比例,函數的自變量
成正比例,函數的自變量![]() 的取值范圍是
的取值范圍是![]() ,且當
,且當![]() 或
或![]() 時,
時,![]() 的值均為
的值均為![]() 。
。
請對該函數及其圖象進行如下探究:
(1)解析式探究:根據給定的條件,可以確定出該函數的解析式為: .
(2)函數圖象探宄:①根據解析式,選取適當的自變量![]() ,并完成下表:
,并完成下表:
|
| ... | ||||||||
| ... |
②根據表中數據,在如圖所示的平面直角坐標系中描點,并畫出函數圖象.
(3)結合畫出的函數圖象,解決問題:
①當![]() ,
,![]() ,
,![]() 時,函數值分別為
時,函數值分別為![]() ,則
,則![]() 的大小關系為: (用“
的大小關系為: (用“![]() ”或“
”或“![]() ”表示)
”表示)
②若直線![]() 與該函數圖象有兩個交點,則
與該函數圖象有兩個交點,則![]() 的取值范圍是 ,此時,
的取值范圍是 ,此時,![]() 的取值范圍是 .
的取值范圍是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是二次函數y=ax2+bx+c的圖象的一部分,對稱軸是直線x=1.
①b2>4ac; ②4a+2b+c<0;③不等式ax2+bx+c>0的解集是x≥3.5;④若(﹣2,y1),(5,y2)是拋物線上的兩點,則y1<y2.上述4個判斷中,正確的是( )
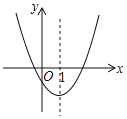
A.①②B.①②④C.①③④D.②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知∠AOB=60°,半徑為2![]() 的⊙M與邊OA、OB相切,若將⊙M水平向左平移,當⊙M與邊OA相交時,設交點為E和F,且EF=6,則平移的距離為____.
的⊙M與邊OA、OB相切,若將⊙M水平向左平移,當⊙M與邊OA相交時,設交點為E和F,且EF=6,則平移的距離為____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知∠AOB=60°,半徑為2![]() 的⊙M與邊OA、OB相切,若將⊙M水平向左平移,當⊙M與邊OA相交時,設交點為E和F,且EF=6,則平移的距離為____.
的⊙M與邊OA、OB相切,若將⊙M水平向左平移,當⊙M與邊OA相交時,設交點為E和F,且EF=6,則平移的距離為____.
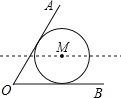
查看答案和解析>>
科目:初中數學 來源: 題型:
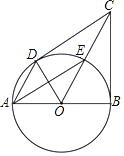
【題目】如圖,已知D是⊙O上一點,AB是直徑,∠BAD的平分線交⊙O于點E,⊙O的切線BC交OE的延長線于點C,連接OD,CD.
(1)求證:CD⊥OD.
(2)若AB=2,填空:
①當CE= 時,四邊形BCDO是正方形.
②作△AEO關于直線OE對稱的△FEO,連接BF,BE,當四邊形BEOF是菱形時,求CE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在每個小正方形邊長為1的網格中,點A,B,C均在格點上.
(Ⅰ)AC的長度等于_____;
(Ⅱ)在圖中有一點P,若連接AP,PB,PC,滿足AP平分∠A,且PC=PB,請在如圖所示的網格中,用無刻度的直尺,畫出點P,并簡要說明點P的位置是如何找到的(不要求證明)_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
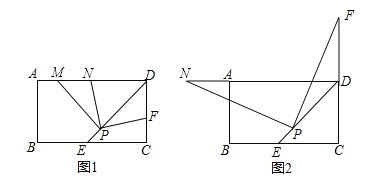
【題目】矩形ABCD中,DE平分∠ADC交BC邊于點E,P為DE上的一點(PE<PD),PM⊥PD,PM交AD邊于點M.
(1)若點F是邊CD上一點,滿足PF⊥PN,且點N位于AD邊上,如圖1所示.
求證:①PN=PF;②DF+DN=![]() DP;
DP;
(2)如圖2所示,當點F在CD邊的延長線上時,仍然滿足PF⊥PN,此時點N位于DA邊的延長線上,如圖2所示;試問DF,DN,DP有怎樣的數量關系,并加以證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知![]() 、
、![]() 兩點在反比例函數
兩點在反比例函數![]() 的圖象上,下列三個命題:①若
的圖象上,下列三個命題:①若![]() ,則
,則![]() ;②若
;②若![]() ,
,![]() ,則
,則![]() ;③過
;③過![]() 、
、![]() 兩點的直線與
兩點的直線與![]() 軸、
軸、![]() 軸分別交于
軸分別交于![]() 、
、![]() 兩點,連接
兩點,連接![]() 、
、![]() ,則
,則![]() .其中真命題個數是( )
.其中真命題個數是( )
A.0B.1C.2D.3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com