
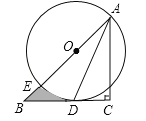
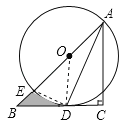
【題目】如圖,在Rt△ABC中,∠C=90°,AC=BC,點O在AB上,經過點A的⊙O與BC相切于點D,交AB于點E.
(1)求證:AD平分∠BAC;
(2)若CD=1,求圖中陰影部分的面積(結果保留π).
【答案】(1)證明見解析;(2)![]() .
.
【解析】試題分析:(1)連接DE,OD.利用弦切角定理,直徑所對的圓周角是直角,等角的余角相等證明∠DAO=∠CAD,進而得出結論;
(2)根據等腰三角形的性質得到∠B=∠BAC=45°,由BC相切⊙O于點D,得到∠ODB=90°,求得OD=BD,∠BOD=45°,設BD=x,則OD=OA=x,OB=![]() x,根據勾股定理得到BD=OD=
x,根據勾股定理得到BD=OD=![]() ,于是得到結論.
,于是得到結論.
試題解析:解:(1)證明:連接DE,OD.
∵BC相切⊙O于點D,∴∠CDA=∠AED,∵AE為直徑,∴∠ADE=90°,∵AC⊥BC,∴∠ACD=90°,∴∠DAO=∠CAD,∴AD平分∠BAC;
(2)∵在Rt△ABC中,∠C=90°,AC=BC,∴∠B=∠BAC=45°,∵BC相切⊙O于點D,∴∠ODB=90°,∴OD=BD,∴∠BOD=45°,設BD=x,則OD=OA=x,OB=![]() x,∴BC=AC=x+1,∵AC2+BC2=AB2,∴2(x+1)2=(
x,∴BC=AC=x+1,∵AC2+BC2=AB2,∴2(x+1)2=(![]() x+x)2,∴x=
x+x)2,∴x=![]() ,∴BD=OD=
,∴BD=OD=![]() ,∴圖中陰影部分的面積=S△BOD﹣S扇形DOE=
,∴圖中陰影部分的面積=S△BOD﹣S扇形DOE=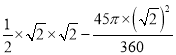 =
=![]() .
.


科目:初中數學 來源: 題型:
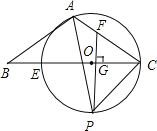
【題目】如圖,在△ABC 中,AB=AC,∠BAC=120°,E 為 BC 上一點,以 CE 為直徑作⊙O 恰好經過 A、C 兩點, PF⊥BC 交 BC 于點 G,交 AC 于點 F.
(1)求證:AB 是⊙O 的切線;
(2)如果 CF =2,CP =3,求⊙O 的直徑 EC.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】老師在黑板上出了一道解方程的題![]() ,小明馬上舉手,要求到黑板上做,他是這樣做的:
,小明馬上舉手,要求到黑板上做,他是這樣做的:
![]() ……………… …①
……………… …①
![]() …………………… …②
…………………… …②
![]() …………………… …③
…………………… …③
![]() ………………………………… ④
………………………………… ④
![]() ………………………………… ⑤
………………………………… ⑤
老師說:小明解一元一次方程的一般步驟都知道卻沒有掌握好,因此解題時有一步出現了錯誤,請你指出他錯在 (填編號);
然后,你自己細心地解下面的方程:![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學對全校1200名學生進行“校園安全知識”的教育活動,從1200名學生中隨機抽取部分學生進行測試,成績評定按從高分到低分排列分為![]() ,
, ![]() ,
, ![]() ,
, ![]() 四個等級,繪制了圖①、圖②兩幅不完整的統計圖.請結合圖中所給信息解答下列問題:
四個等級,繪制了圖①、圖②兩幅不完整的統計圖.請結合圖中所給信息解答下列問題:
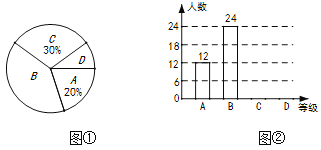
(1)求本次被抽查的學生共有多少名?
(2)將條形統計圖和扇形統計圖補充完整;
(3)求扇形統計圖中“![]() ”所在的扇形圓心角的度數;
”所在的扇形圓心角的度數;
(4)估計全校“![]() ”等級的學生有多少名?
”等級的學生有多少名?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分別是BG,AC的中點.
(1)求證:DE=DF,DE⊥DF;
(2)連接EF,若AC=10,求EF的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
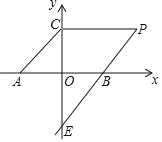
【題目】如圖,直線y=x+3與x軸、y軸分別相交于A、C兩點,過點B(6,0),E(0,﹣6)的直線上有一點P,滿足∠PCA=135°.
(1)求證:四邊形ACPB是平行四邊形;
(2)求直線BE的解析式及點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小聰在復習過程中,發現數軸上線段的長度可以用線段端點表示的數進行減法運算得到,例:
如圖1,線段![]() ,線段
,線段![]() ,
,

線段![]() ,線段
,線段![]()
結論:數軸上任意兩點表示的數分別為:![]() ,
,![]() (
(![]() ),則這兩點間的距離為:
),則這兩點間的距離為:![]() (即:較大的數減去較小的數).
(即:較大的數減去較小的數).
嘗試應用:
(1)若數軸上點![]() ,點
,點![]() 代表的數分別是-3,-1,則
代表的數分別是-3,-1,則![]() ______.
______.
(2)把一條數軸在數![]() 處對折,表示-9和3兩數的點恰好互相重合,此時
處對折,表示-9和3兩數的點恰好互相重合,此時![]() ______.
______.
(3)數軸上的兩個點之間的距離為6,其中一個點表示的數為3,另一個點表示的數為![]() ,則
,則![]() ______.
______.
問題解決:
(4)如圖2,點![]() 表示數
表示數![]() ,點
,點![]() 表示-2,點
表示-2,點![]() 表示
表示![]() 且
且![]() ,問點
,問點![]() 和點
和點![]() 分別表示什么數?為什么?
分別表示什么數?為什么?

(5)上述(4)的條件下,圖2所示的數軸上,是否存在滿足條件的點![]() ,使用
,使用![]() ?
?
若存在,請直接寫出![]() 所表示的數,若不存在,請說明理由?(點
所表示的數,若不存在,請說明理由?(點![]() 不與點
不與點![]() ,點
,點![]() ,點
,點![]() 重合)
重合)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,D、E是BC邊上的點,BD:DE:EC=3:2:1,M在AC邊上,CM:MA=1:2,BM交AD,AE于H,G,則BH:HG:GM等于( )
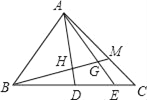
A. 3:2:1 B. 5:3:1 C. 25:12:5 D. 51:24:10
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com